Estimating Bid-Ask Spreads Using OHLCÂ Prices
Efficient Estimation of bid-ask spreads from open, high, low, and close prices using moment conditions, rolling windows, and generalized method of moments weighting
Most traders underestimate how much bid-ask spreads eat into their profits. Even small spreads can significantly impact execution costs, especially in low-liquidity markets.Â
Yet, accurately measuring spreads isn’t straightforward — especially when relying on open, high, low, and close (OHLC) prices instead of full order book data.
A more accurate approach is outlined in the work of Ardia, Guidotti, and Kroencke (2024), who propose an estimator that improves spread measurement using Generalized Method of Moments and OHLC price transformations.Â
This method corrects for price discreteness and minimizes estimation variance. Unlike older models, it adapts to market conditions in real-time. It’s a powerful tool for traders, quants, and financial researchers.
In this article, we’ll break down the problem, explain the math behind the estimator, and show how to implement it in Python.Â
Finally, we’ll analyze real-world bid-ask spreads for AAPL stock to get insights into transaction costs and liquidity.
1. Why Traditional Spread Estimators Fail
Traditional methods rely on assumptions that often do not hold in real markets. This leads to biased and inconsistent estimates.
Roll (1984) Estimator
One of the most cited models, the Roll estimator, derives the spread from the negative serial covariance of price changes:
Ct is the closing price at time t. This method assumes:
- all trades occur at observed prices a
- the bid-ask bounce is the only source of price variation.Â
However, in real markets:
- Prices are not observed continuously.
- There may be zero or few trades in a given period.
- Trades are executed at various price levels, not just at the close.
Corwin & Schultz (2012) High-Low Estimator
To reduce variance, Corwin & Schultz (2012) proposed an estimator using high and low prices:
B represents the variance of log high-low price ratios. This model assumes:
- High prices correspond to buys, and low prices to sells.
- Price movements follow a geometric Brownian motion.
Both assumptions fail in markets with price jumps and volatility clustering, which makes it an unreliable estimator.
Abdi & Ranaldo (2017) OHLC Estimator
An improvement by Abdi & Ranaldo (2017) integrates closing, high, and low prices:
where ηt is the mid-price. While this reduces bias, it still fails to fully account for discrete price observations. This leads to inaccuracies in low-trading-frequency markets.
2. A More Accurate Approach: Using OHLCÂ Prices
Ardia et al. (2024) address these limitations by incorporating all OHLC price observations.Â
Their key innovation uses moment conditions to isolate bid-ask spread effects while controlling for fundamental price variations.Â
The approach defines multiple log-returns based on OHLC prices:
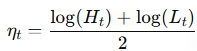
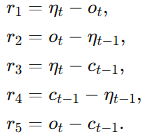
ot, ct, Ht, Lt are log-transformed open, close, high, and low prices.
A key correction is introduced via an indicator for price variation, which adjusts for cases where prices remain unchanged:
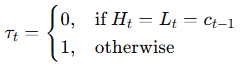
The method avoids overestimating spreads when price changes are minimal to address a key weakness in prior models.
How the Rolling Estimator Works
This estimator improves bid-ask spread measurement by leveraging OHLC prices and a rolling window to track liquidity trends dynamically.
The spread estimate is computed as:
ηt is the midpoint log-price, and τt​ accounts for price variation.
Key advantages:
- GMM weighting minimizes variance:
- Rolling updates ensure time-varying accuracy.
- Non-negativity is enforced as (resets negative estimates to zero):
This method reduces bias and improves precisio. It outperforms traditional estimators, especially in low-liquidity markets.
3. Implementation in Python
The following implementation borrows its core logic from the original repository by Ardia et al. (2024).Â
Newsletter