Manual trend lines are subjective and slow. This algorithmic method finds direction, strength, and confluence

Most trend channels anchor to arbitrary points, assume symmetry, and fail to adapt when the market shifts.

Traders rely on them for clarity, only to be misled by breakouts that weren’t real and reversals that weren’t clean.

To address this issue, we implement multi-anchored linear regression channels that adapt to real price structure. These channels aren’t static, they respond to market highs, lows, and consolidation periods.

Even better, they highlight confluence zones where different trend signals align. Main output of this analysis:

We provide end-to-end implemention in a single Python script, to generate:

Three distinct regression channels from meaningful anchor points
Statistical metrics like slope, R², and correlation for each trendline
Visual markers for overextended moves, trend exhaustion, and structural agreement

Google Notebook provided below.

1. The Multi-Anchor Approach

Linear regression channels are only as useful as their anchor points. Instead of picking a fixed lookback window, this method selects three distinct anchors based on real price behavior:

1.1 Highest High → Potential Resistance

We search for the most recent bar where price hit its highest high. This point marks exhaustion. Anchoring from here captures descending resistance.

For example, If the highest high over the last 800 bars occurred 120 bars ago, we fit a regression line starting from that bar to today.

1.2 Lowest Low → Potential Support

Same logic, inverted. We locate the lowest low in the recent past. This anchor signals structural support and potential bounce zones.

For example, If the lowest low was 95 bars ago, we regress from that bar forward.

3.3 Flattest Slope → Neutral Phase

This anchor finds the segment where price shows the least directional bias. It identifies sideways consolidation.

We scan recent windows and select the one where the regression slope β1 is closest to zero:

The window with ∣β1∣≈0 becomes the neutral anchor. Each anchor yields a separate regression channel. For each:

Midline is the fitted regression line: y=β0+β1x
Residuals measure deviation from the line: ϵ=y−(β0+β1x)
Standard deviation of residuals defines channel width:

Channel boundaries:

Upper: y+Dσ
Lower: y−Dσ

(D is a deviation multiplier, e.g., 2)

Why Use All Three Anchors?

Each provides a different lens on trend:

Highest high shows declining pressure (momentum).
Lowest low highlights bullish structure (mean reversion).
Flattest slope finds indecision zones (range behavior).

When multiple channels align around the same slope or price region, that’s confluence.

Confluence reduces noise. It highlights agreement between distinct price behaviors. If all channels point up, the trend has confirmation. If they diverge, it flags instability or transition.

2. Python Implementation

The workflow is modular and easy to extend for custom anchors or asset classes.

2.1 Configuration and Parameters

Define the stock symbol, date range, and analysis settings. These include:

MAX_BARS: How far back to search for anchors.
DEV_MULT: Channel width multiplier for standard deviation.
USE_LOG_SCALE: Option to normalize trends via log(price).
USE_EXP_WEIGHT: Gives more weight to recent data in the regression.

				
					import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from typing import Tuple

# Settings
TICKER = "NVDA"  # Symbol to analyze
START_DATE = "2022-01-01"
END_DATE = "2026-01-01"
MAX_BARS = 2000  # Max lookback window for anchor search
DEV_MULT = 2.0   # Width of channel = ±stdev * this multiplier
USE_LOG_SCALE = False  # Enable log(price) transformation
USE_EXP_WEIGHT = False  # Use exponential sample weights if Preferable (use with catious)
ANCHORS = ["BarHighest", "BarLowest", "SlopeZero"]
CHANNEL_COLORS = ["lime", "orange", "cyan"]

2.2 Helper Functions

If log scaling is enabled, price is transformed using:

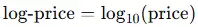
This can help stabilize variance and linearize exponential trends. We reverse the transformation before plotting.

				
					def transform_price(p: pd.Series) -> pd.Series:
    """Transform price data using log scale if enabled."""
    return np.log10(p) if USE_LOG_SCALE else p

def inverse_transform_price(p: np.ndarray) -> np.ndarray:
    """Inverse transform the price data."""
    return np.power(10, p) if USE_LOG_SCALE else p

def exponential_weights(n: int, decay: float = 0.90) -> np.ndarray:
    """Return exponential weights for a given length."""
    return decay ** np.arange(n)[::-1]

Anchor Detection

Each anchor type determines the window length for the regression:

BarHighest: Finds how many bars ago the highest high occurred.
BarLowest: Same for the lowest low.
SlopeZero: Searches for the segment where the regression slope is closest to zero.

Draw Trend Lines Algorithmically with Multi-Anchored Regressions

Manual trend lines are subjective and slow. This algorithmic method finds direction, strength, and confluence