End-to-end Implementation with buy and sell signals
Trend indicators, a key component in technical analysis, offer insights into market directions and strength, allowing traders to make informed decisions.
While the theoretical understanding of these indicators is vital, the real power lies in their practical application. This article delves into the practical side of trend indicators, focusing on their implementation in Python
In this article, we provide ready-to-use Python implementations for key trend indicators:
- Moving Averages (SMA and EMA)
- MACD
- ADX
- Parabolic SAR
- Ichimoku Cloud
- ZigZag Indicator
Each offers unique insights — from smoothing prices for trend clarity to highlighting momentum shifts and pinpointing entry/exit points.
2. Python Implementation
2.1 Moving Averages (SMA, EMA)
Simple Moving Average (SMA) and Exponential Moving Average (EMA) are foundational tools in trend analysis. These tools serve as important trend indicators.
SMA calculates the average price over a specific period. This provides a smoothed representation of price movement. EMA gives more weight to recent prices, making it more responsive to new information.
The SMA is the arithmetic mean of prices over a specified number of past days. This essentially averages the price data. For a 20-day SMA, it sums up the closing prices of the last 20 days and divides by 20.
Equation 1. Mathematical Representation of the Simple Moving Average (SMA) for a Defined Period.
The EMA gives more weight to recent prices, making it quicker to respond to price changes than the SMA. It weights the most recent price based on the selected time period. The formula blends previous EMA values with a smoothing factor for recent prices.
Equation 2. Formula for the Exponential Moving Average (EMA) with Smoothing Factor α.
Application of Moving Averages
While both SMA and EMA are crucial for trend analysis, the EMA’s responsiveness to recent price changes allows traders to potentially catch trends earlier than with the SMA.
This difference can be particularly useful in volatile markets, where the EMA can help traders react more quickly to sudden price movements. Additionally, the concept of crossovers between short-term and long-term moving averages (e.g., 20-day and 50-day) serves as a fundamental signal for trend reversals.
A crossover above suggests an uptrend (buy signal), while a crossover below indicates a downtrend (sell signal). This method, especially when confirmed by other indicators, can offer robust entry and exit strategies. Understanding SMA and EMA crossovers enhances trading strategy insights and decision-making
import yfinance as yf
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
# Download historical data for a stock
symbol = 'AAPL' # Example stock symbol
start_date = '2020-01-01'
end_date = '2024-11-01'
data = yf.download(symbol, start=start_date, end=end_date)
# Calculate SMAs
short_window = 20
long_window = 50
data['SMA20'] = data['Close'].rolling(window=short_window, min_periods=1).mean()
data['SMA50'] = data['Close'].rolling(window=long_window, min_periods=1).mean()
# Calculate EMAs
data['EMA20'] = data['Close'].ewm(span=short_window, adjust=False).mean()
data['EMA50'] = data['Close'].ewm(span=long_window, adjust=False).mean()
# Detect SMA Crossovers
data['SMA_Cross_Up'] = (data['SMA20'] > data['SMA50']) & (data['SMA20'].shift(1) < data['SMA50'].shift(1))
data['SMA_Cross_Down'] = (data['SMA20'] < data['SMA50']) & (data['SMA20'].shift(1) > data['SMA50'].shift(1))
# Detect EMA Crossovers
data['EMA_Cross_Up'] = (data['EMA20'] > data['EMA50']) & (data['EMA20'].shift(1) < data['EMA50'].shift(1))
data['EMA_Cross_Down'] = (data['EMA20'] < data['EMA50']) & (data['EMA20'].shift(1) > data['EMA50'].shift(1))
# Plotting
fig, axs = plt.subplots(1, 2, figsize=(16, 4), sharex=True, sharey=True)
# Configure date formatting
for ax in axs:
ax.xaxis.set_major_locator(mdates.AutoDateLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
# SMA Plot
axs[0].plot(data.index, data['Close'], label='Close Price', color='black', alpha=0.75)
axs[0].plot(data.index, data['SMA20'], label='SMA 20 Days', color='blue', alpha=0.75)
axs[0].plot(data.index, data['SMA50'], label='SMA 50 Days', color='red', alpha=0.75)
axs[0].scatter(data.index[data['SMA_Cross_Up']], data['Close'][data['SMA_Cross_Up']], label='Buy Signal', marker='^', color='green', s=100)
axs[0].scatter(data.index[data['SMA_Cross_Down']], data['Close'][data['SMA_Cross_Down']], label='Sell Signal', marker='v', color='red', s=100)
axs[0].set_title(f'{symbol} SMA Crossover Strategy')
axs[0].legend()
axs[0].grid()
# EMA Plot
axs[1].plot(data.index, data['Close'], label='Close Price', color='black', alpha=0.75)
axs[1].plot(data.index, data['EMA20'], label='EMA 20 Days', color='blue', alpha=0.75)
axs[1].plot(data.index, data['EMA50'], label='EMA 50 Days', color='red', alpha=0.75)
axs[1].scatter(data.index[data['EMA_Cross_Up']], data['Close'][data['EMA_Cross_Up']], label='Buy Signal', marker='^', color='green', s=100)
axs[1].scatter(data.index[data['EMA_Cross_Down']], data['Close'][data['EMA_Cross_Down']], label='Sell Signal', marker='v', color='red', s=100)
axs[1].set_title(f'{symbol} EMA Crossover Strategy')
axs[1].legend()
axs[1].grid()
# Improve layout and plot
plt.tight_layout()
plt.show()
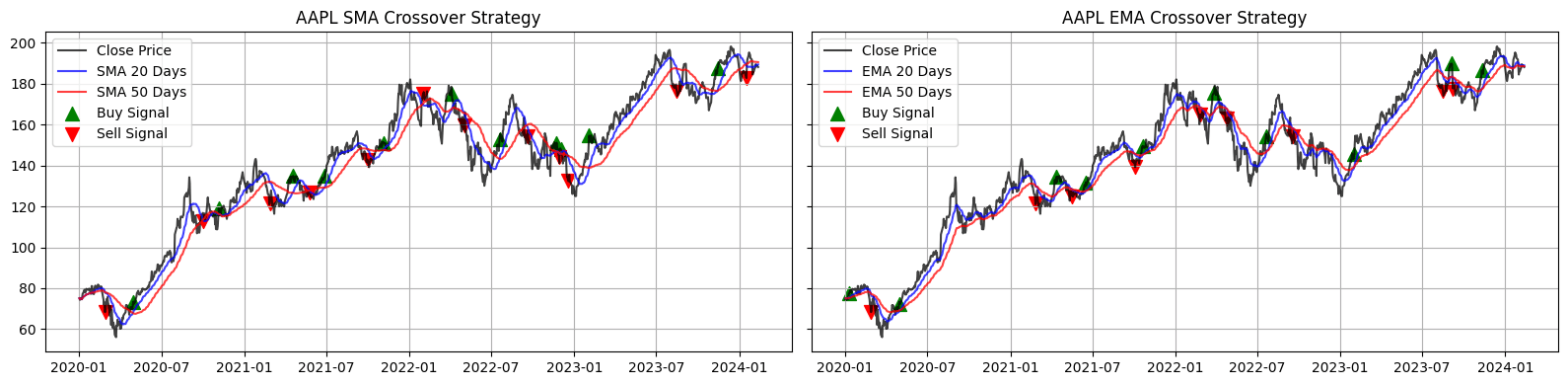
Figure. 1: The dual charts display the closing prices alongside their 20-day and 50-day SMAs and EMAs, illustrating buy signals (green arrows) at SMA and EMA crossovers above the longer average and sell signals (red arrows) at crossovers below. These visual cues highlight the utility of moving averages in trend identification and momentum assessment.
We suggest readers to get acquinted with more diverse and advanced moving average methods. The following articles are a good starting point:
Top 36 Moving Average Methods For Stock Prices in Python
The Art Of Crossing Over Moving Averages In Python
2.2 Moving Average Convergence Divergence (MACD)
The MACD is a trend-following momentum indicator that shows the relationship between two moving averages of a security’s price nd is one of the most widely used trend indicators in technical analysis. It consists of the MACD line, the signal line, and the MACD histogram.
The MACD line is calculated by subtracting the 26-day Exponential Moving Average (EMA) from the 12-day EMA. The signal line is the 9-day EMA of the MACD line. The histogram represents the difference between the MACD line and its signal line.
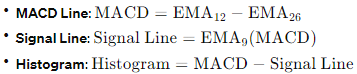
Equation 3. MACD Formulas: The MACD line indicates momentum by subtracting the 26-day EMA from the 12-day EMA. The signal line, a 9-day EMA of the MACD, helps identify turns. The histogram measures the gap between the MACD and its signal line, providing insights into trend strength and direction..
Application of MACD
An essential aspect of the MACD indicator is its ability to identify momentum changes before they are reflected in the price of an asset, offering traders a leading signal to potential market moves.
The crossing of the MACD line over the signal line can serve as an early indication of a changing trend, providing opportunities for entry or exit before the bulk of the move occurs.
Furthermore, the MACD histogram is particularly useful for spotting divergences from price action, a scenario where the price may be making new highs or lows that are not confirmed by the MACD.
This divergence can often precede a reversal, making the MACD a powerful tool for predicting the end of an existing trend and the start of a new one. Understanding these nuances allows traders to leverage MACD not just for trend following but also for predicting potential reversals.
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
from ta.trend import MACD
def fetch_stock_data(ticker, start_date, end_date):
stock_data = yf.download(ticker, start=start_date, end=end_date)
return stock_data
def plot_macd_signals(dates, prices, macd_line, signal_line, macd_histogram):
buy_signals = (macd_line > signal_line) & (macd_line.shift(1) <= signal_line.shift(1))
sell_signals = (macd_line < signal_line) & (macd_line.shift(1) >= signal_line.shift(1))
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(22, 9), sharex=True)
ax1.plot(dates, prices, color='g', label='Stock Price', zorder=3)
ax1.scatter(dates[buy_signals], prices[buy_signals], marker='^', color='b', label='Buy', zorder=4, s=150)
ax1.scatter(dates[sell_signals], prices[sell_signals], marker='v', color='r', label='Sell', zorder=5, s=150)
for date in dates[buy_signals]:
ax1.axvline(date, color='b', alpha=0.5, linestyle='--', linewidth=0.5)
for date in dates[sell_signals]:
ax1.axvline(date, color='r', alpha=0.5, linestyle='--', linewidth=0.5)
ax1.set_ylabel('Stock Price')
ax1.legend(loc='upper left')
ax2.plot(dates, macd_line, label='MACD', color='b', alpha=0.3, zorder=1)
ax2.plot(dates, signal_line, label='Signal', color='r', alpha=0.3, zorder=2)
ax2.bar(dates, macd_histogram, label='MACD Histogram', color=np.where(macd_histogram >= 0, 'g', 'r'), alpha=0.3)
for date in dates[buy_signals]:
ax2.axvline(date, color='b', alpha=0.5, linestyle='--', linewidth=0.5)
for date in dates[sell_signals]:
ax2.axvline(date, color='r', alpha=0.5, linestyle='--', linewidth=0.5)
ax2.set_ylabel('MACD')
ax2.legend(loc='upper left')
plt.title(f'Stock Price and MACD for {ticker}')
plt.xlabel('Date')
plt.tight_layout()
plt.show()
ticker = "AFX.DE"
start_date = "2020-01-01"
end_date = "2023-12-30"
stock_data = fetch_stock_data(ticker, start_date, end_date)
prices = stock_data['Close']
macd_indicator = MACD(prices)
macd_line = macd_indicator.macd()
signal_line = macd_indicator.macd_signal()
macd_histogram = macd_indicator.macd_diff()
plot_macd_signals(prices.index, prices, macd_line, signal_line, macd_histogram)
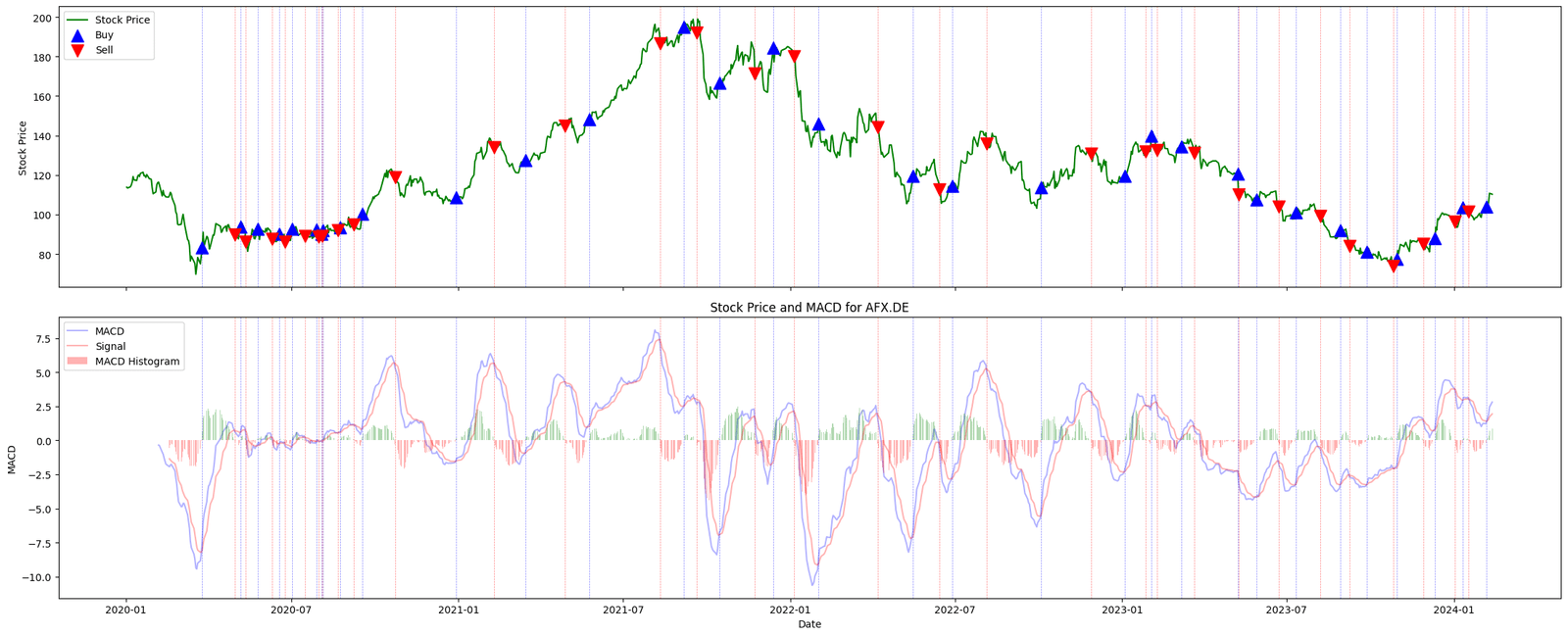
Figure. 2: The graph presents stock price with corresponding MACD signals. Buy signals are depicted with blue upward arrows when the MACD line crosses above the signal line, and sell signals with red downward arrows on crossings below, illustrating the indicator's utility in identifying potential trend reversals and momentum shifts. The MACD histogram, varying above and below zero, offers a visual representation of the momentum's strength, with green bars indicating increasing bullish momentum and red bars signaling bearish momentum.
2.3 Average Directional Movement Index (ADX)
The ADX is a technical analysis tool used to quantify the strength of a trend. It is derived from the Directional Movement Index (DMI) system, which includes two other indicators: the Positive Directional Indicator (+DI) and the Negative Directional Indicator (-DI). The ADX stands out as a crucial tool among trend indicators.
The ADX itself is a smoothed average of the absolute difference between +DI and -DI, normalized to a scale of 0 to 100. The formula for calculating each component is as follows:
- Calculate the differences between consecutive highs and lows to determine directional movements (+DM and -DM).
- Calculate the True Range (TR), the maximum of today’s high-low range, the high minus the previous close, and the low minus the previous close.
- Normalize +DM and -DM by the TR to get +DI and -DI.
- The ADX is then calculated by smoothing the differences between +DI and -DI over a specified period (usually 14 days) and normalizing the result.
True Range (TR):
Directional Movements:
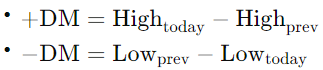
Directional Indicators:
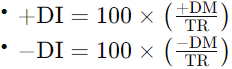
Average Directional Index (ADX):
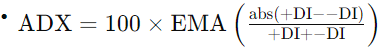
Figure. 4: ADX Formula: Averages the difference between +DI and -DI, normalized to indicate trend strength. High ADX values suggest strong trends, while low values indicate weaker trends.
Application of ADX
The ADX excels in filtering out market noise by focusing solely on trend strength, regardless of direction. A crucial insight into its application is that the ADX can help distinguish between conditions conducive to trend-following strategies and those that are more suited to range-bound trading approaches.
For instance, an ADX reading above 25 suggests that a trend-following strategy might be more appropriate, whereas readings below 20 indicate a lack of strong trend, potentially favoring range-bound strategies.
Furthermore, the interplay between +DI and -DI alongside the ADX enhances the indicator’s utility, allowing traders to not only gauge the strength of a trend but also to anticipate potential reversals based on crossovers of the DI lines.
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
import numpy as np
# Download historical data as dataframe
ticker = "ASML.AS"
df = yf.download(ticker, start='2020-01-01', end='2024-12-30')
def calculate_ADX(df, n):
df['H-L'] = abs(df['High'] - df['Low'])
df['H-PC'] = abs(df['High'] - df['Close'].shift(1))
df['L-PC'] = abs(df['Low'] - df['Close'].shift(1))
df['TR'] = df[['H-L', 'H-PC', 'L-PC']].max(axis=1)
df['+DM'] = np.where((df['High'] > df['High'].shift(1)), df['High'] - df['High'].shift(1), 0)
df['-DM'] = np.where((df['Low'] < df['Low'].shift(1)), df['Low'].shift(1) - df['Low'], 0)
TRn = []
DMpn = []
DMnn = []
TR = df['TR'].tolist()
DMp = df['+DM'].tolist()
DMn = df['-DM'].tolist()
for i in range(len(df)):
if i < n:
TRn.append(np.NaN)
DMpn.append(np.NaN)
DMnn.append(np.NaN)
elif i == n:
TRn.append(df['TR'].rolling(n).sum().tolist()[n])
DMpn.append(df['+DM'].rolling(n).sum().tolist()[n])
DMnn.append(df['-DM'].rolling(n).sum().tolist()[n])
elif i > n:
TRn.append(TRn[i-1] - (TRn[i-1]/n) + TR[i])
DMpn.append(DMpn[i-1] - (DMpn[i-1]/n) + DMp[i])
DMnn.append(DMnn[i-1] - (DMnn[i-1]/n) + DMn[i])
df['TRn'] = np.array(TRn)
df['+DMn'] = np.array(DMpn)
df['-DMn'] = np.array(DMnn)
df['+DI'] = 100 * (df['+DMn']/df['TRn'])
df['-DI'] = 100 * (df['-DMn']/df['TRn'])
df['DIdiff'] = abs(df['+DI'] - df['-DI'])
df['DIsum'] = df['+DI'] + df['-DI']
df['DX'] = 100 * (df['DIdiff']/df['DIsum'])
ADX = []
DX = df['DX'].tolist()
for j in range(len(df)):
if j < 2*n-1:
ADX.append(np.NaN)
elif j == 2*n-1:
ADX.append(df['DX'][j-n+1:j+1].mean())
elif j > 2*n-1:
ADX.append(((n-1)*ADX[j-1] + DX[j])/n)
df['ADX'] = np.array(ADX)
return df['ADX']
calculate_ADX(df, 14)
# Generate signals
df['signal'] = 0
df.loc[(df['ADX']>25) & (df['+DI']>df['-DI']), 'signal'] = 1
df.loc[(df['ADX']>25) & (df['-DI']>df['+DI']), 'signal'] = -1
# Identify the points where the signals change from 0 to 1 or -1
#df['buy_signal'] = ((df['signal'] == 1) & (df['signal'].shift(1) == 0))
#df['sell_signal'] = ((df['signal'] == -1) & (df['signal'].shift(1) == 0))
# Plotting
fig, (ax1, ax2) = plt.subplots(2, figsize=(30, 14))
# Plot the closing price
df['Close'].plot(ax=ax1)
ax1.set_ylabel('Price')
# Plot the entry and exit points
#ax1.plot(df[df['buy_signal']].index, df['Close'][df['buy_signal']], '^', markersize=10, color='g', label='buy')
#ax1.plot(df[df['sell_signal']].index, df['Close'][df['sell_signal']], 'v', markersize=10, color='r', label='sell')
ax1.legend()
# Plot the ADX, +DI, -DI
df['ADX'].plot(ax=ax2, color='black', label='ADX')
df['+DI'].plot(ax=ax2, color='green', label='+DI')
df['-DI'].plot(ax=ax2, color='red', label='-DI')
ax2.set_ylabel('ADX')
ax2.legend()
# Show the plot
plt.show()
'''
The ADX line shows the strength of the trend. Generally, an ADX above 25 is considered to indicate a strong trend, while an ADX below 20 suggests a weak or non-trending market.
The +DI and -DI lines can help identify the direction of the trend. When +DI is above -DI, it suggests an upward trend, and when -DI is above +DI, it suggests a downward trend.
The trading signals indicate potential points to enter or exit the market. A signal of 1 suggests a potential buying opportunity (entering a long position or closing a short position),
while a signal of -1 suggests a potential selling opportunity (entering a short position or closing a long position).
These signals are based on a very basic strategy and may not always be accurate or profitable.
'''
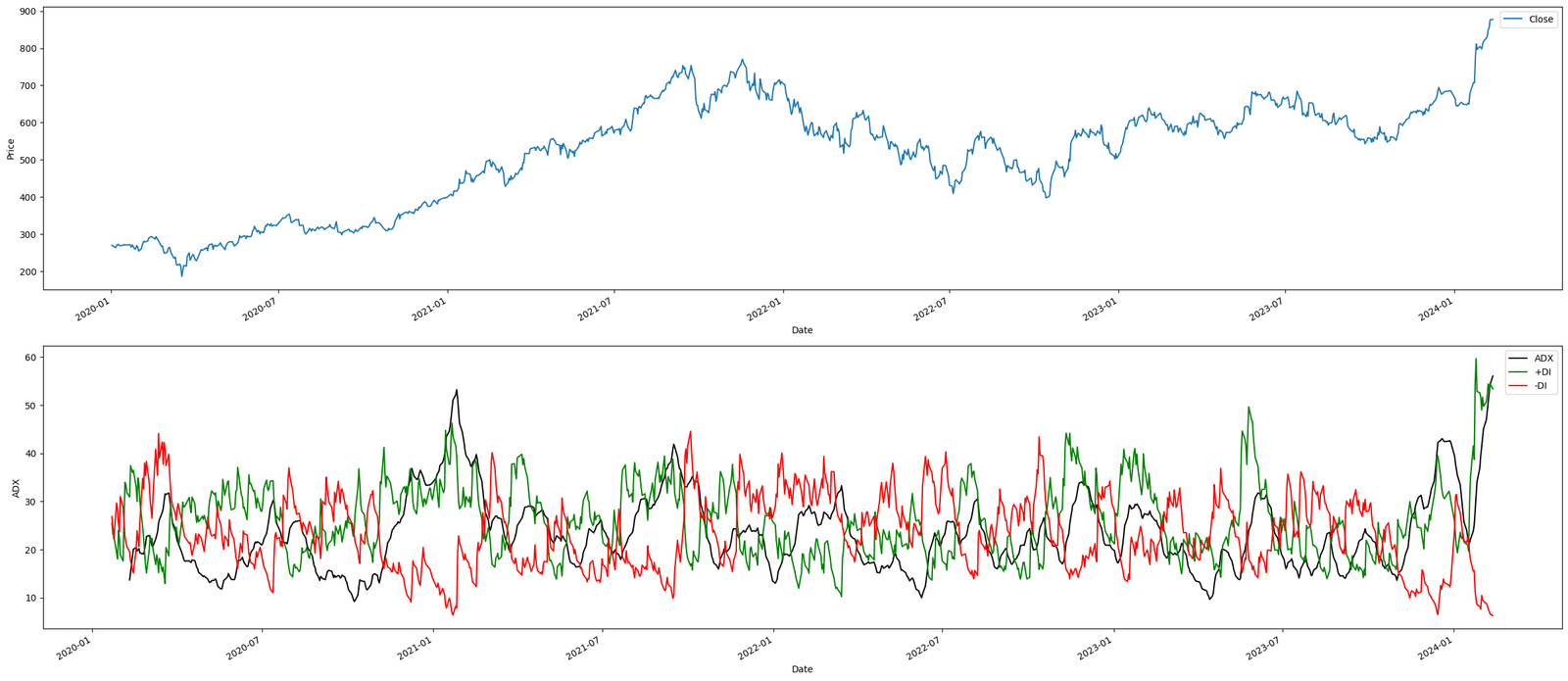
Figure. 3: The chart displays closing prices along with the ADX, +DI, and -DI lines. The ADX line quantifies trend strength, with values above 25 indicating strong trends. Crossovers between +DI and -DI provide insights into trend direction, with +DI above -DI suggesting bullish conditions and vice versa. The visualization aids in understanding the market's momentum and potential entry or exit points based on trend strength and direction.
2.4 Parabolic SAR (Stop and Reverse)
The Parabolic SAR is a trend-following indicator that provides entry and exit points. The calculation involves an acceleration factor (AF) that increases by a user-defined step each time the extreme point (EP) makes a new high (in an uptrend) or low (in a downtrend). The formula for updating the SAR value is different for uptrends and downtrends.
Uptrend:
Downtrend:
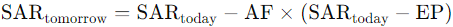
Figure. 5: Parabolic SAR Formula: Calculates future SAR values by adjusting current ones towards the EP at a rate defined by the AF, indicating potential reversals with dots plotted relative to price action.
Application of Parabolic SAR
A key insight of the Parabolic SAR is its effectiveness in trending markets, where it can clearly signal continuation or reversal points. However, its performance may diminish in sideways or choppy markets due to potential false signals.
The Parabolic SAR is especially useful for setting trailing stop losses, as it moves closer to the price as the trend progresses, allowing traders to lock in profits while providing an objective point to exit if the trend reverses.
This dynamic adjustment aligns with the market’s movement, offering a disciplined approach to managing trades based on technical analysis rather than emotion. The indicator’s simplicity and direct visual representation on charts make it an invaluable tool among trend indicators for traders seeking to capitalize on strong trends and minimize losses during reversals.
import yfinance as yf
import ta
import pandas as pd
import numpy as np
# Load the data from yfinance
ticker = "VOW.DE"
df = yf.download(ticker, start="2020-01-01", end="2024-12-30")
# Define the range of values to test for step and max step
step_values = np.arange(0.01, 0.11, 0.01)
max_step_values = np.arange(0.1, 0.31, 0.01)
# Initialize variables to store the best parameters and accuracy
best_step = None
best_max_step = None
best_accuracy = 0
# Loop through the parameter values and backtest the indicator
for step in step_values:
for max_step in max_step_values:
# Calculate the Parabolic SAR with the current parameters
indicator = ta.trend.PSARIndicator(high=df['High'], low=df['Low'], close=df['Close'], step=step, max_step=max_step)
df['PSAR'] = indicator.psar()
# Calculate the buy and sell signals based on the Parabolic SAR
df['Signal'] = np.where(df['Close'] > df['PSAR'], 1, -1)
# Calculate the accuracy of the signals
df['Correct'] = np.where(df['Signal'].shift(1) == df['Signal'], 1, 0)
accuracy = df['Correct'].sum() / len(df)
# Update the best parameters and accuracy if the current values are better
if accuracy > best_accuracy:
best_step = step
best_max_step = max_step
best_accuracy = accuracy
# Calculate the Parabolic SAR
indicator = ta.trend.PSARIndicator(high=df['High'], low=df['Low'], close=df['Close'], step=best_step, max_step=best_max_step)
# Add the indicator to the dataframe
df['PSAR'] = indicator.psar()
# Calculate the buy and sell signals based on the Parabolic SAR
buy_signals = df[df['Close'] > df['PSAR']]['Close']
sell_signals = df[df['Close'] < df['PSAR']]['Close']
# Plot the stock price and the Parabolic SAR with buy and sell signals
fig, ax = plt.subplots(figsize=(30,6))
ax.plot(df['Close'], label='f{ticker} Stock Price')
ax.plot(df['PSAR'], label='Parabolic SAR')
ax.scatter(buy_signals.index, buy_signals.values, color='green', label='Buy')
ax.scatter(sell_signals.index, sell_signals.values, color='red', label='Sell')
ax.legend(loc='upper left')
ax.set(title=f'{ticker} Stock Price with Parabolic SAR and Buy/Sell Signals', xlabel='Date', ylabel='Price')
plt.show()
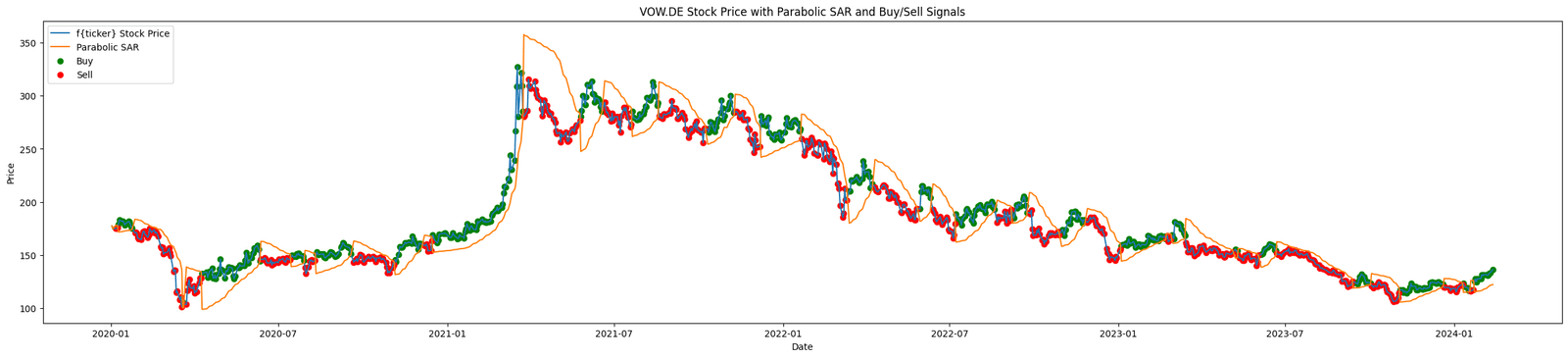
Figure. 4: The chart showcases the stock price overlaid with the Parabolic SAR, highlighted by a series of dots that switch positions relative to the price to indicate trend reversals. Green markers represent buying opportunities when the price moves above the SAR dots, while red markers signal selling or shorting opportunities as the price falls below the SAR dots.
2.5 Ichimoku Cloud
Ichimoku Cloud is a comprehensive indicator that provides information on support/resistance, trend direction, momentum, and potential entry/exit points, all in one glance.
It provides a multi-dimensional view of the market’s price action unlike other trend indicators. It consists of five main components:
- Tenkan-sen (Conversion Line): The average of the highest high and the lowest low over the last 9 periods.
- Kijun-sen (Base Line): The average of the highest high and the lowest low over the last 26 periods.
- Senkou Span A (Leading Span A): The average of the Tenkan-sen and the Kijun-sen, plotted 26 periods ahead.
- Senkou Span B (Leading Span B): The average of the highest high and the lowest low over the past 52 periods, plotted 26 periods ahead.
- Chikou Span (Lagging Span): The closing price plotted 26 periods back.
Related Articles:
Top 6 Volatility Indicators In Python

Newsletter