Finding Today’s Stock Price Pattern in Historical Data
Stock prices change frequently, creating complex data that’s hard to understand. However, through pattern mining in this data, we can uncover valuable insights into future price changes. Specifically, one effective method to spot these patterns is by using a technique called Dynamic Time Warping (DTW).
Moreover, DTW measures the similarity between two time series, even if they differ in length. This feature is especially useful for analyzing stock prices, which can vary widely in their movements and timing. Consequently, by recognizing patterns from the past, we can predict possible future price changes, turning past data into a useful forecasting tool.
In this article, we will explore how to use DTW in Python to find patterns in stock price data. We focus on patterns that closely match recent market trends. Additionally, through strategic visualization, we enhance our understanding of these historical patterns and use them to predict future stock movements.

1. What is Dynamic Time Warping?
Dynamic Time Warping (DTW) originated from speech recognition efforts and provides a specialized approach to time series analysis. It adeptly identifies similarities between temporal sequences that vary in speed and timing. Originally used to understand variations in spoken words, DTW is now also a valuable tool in financial pattern mining.
Consider two temporal sequences, A and B, where A = a1, a2,…, an and B = b1, b2,…, bm. Traditional metrics like Euclidean distance may inaccurately represent the true similarity between A and B if they are out of phase. Formally, the Euclidean distance is given by:
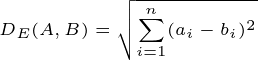
Equation 1. The Euclidean distance DE between two time series A and B of equal length n, where ai and bi are the ith elements of A and B respectively. The Euclidean distance computes the straight-line distance between corresponding points of the time series.
Whereas, DTW offers flexibility in aligning the sequences in a non-linear fashion, minimizing the cumulative distance and therefore, rendering a more accurate representation of their similarity. The DTW distance between A and B is computed as:

Equation 2. The DTW distance between two time series A and B of potentially unequal length. ai and bj(i) denote the elements of A and B at arbitrary indices i and j(i) respectively. DTW allows for optimal alignment between the points of the two time series, thereby enabling a more flexible and context-aware measure of similarity.
Where j (i) represents an alignment function that finds the optimal alignment between elements of A and B, minimizing the cumulative distance. DTW effectively warps the time dimension to align the sequences, ensuring each point in sequence A is matched with the most analogous point in sequence B.
DTW for Mining Patterns in Stock Prices
The pattern of stock prices, propelled by a myriad of factors, generates time series that frequently embodies patterns that could hint at future movements. While some patterns appear overtly similar, others may be subtly analogous with differences in their timing or amplitude.
DTW allows us to compare the similarity between a current price pattern and historical patterns by aligning them optimally in the time dimension. This process enhances our understanding of how current market dynamics mirror historical patterns. These insights, gained through pattern mining, can potentially forecast future price movements.
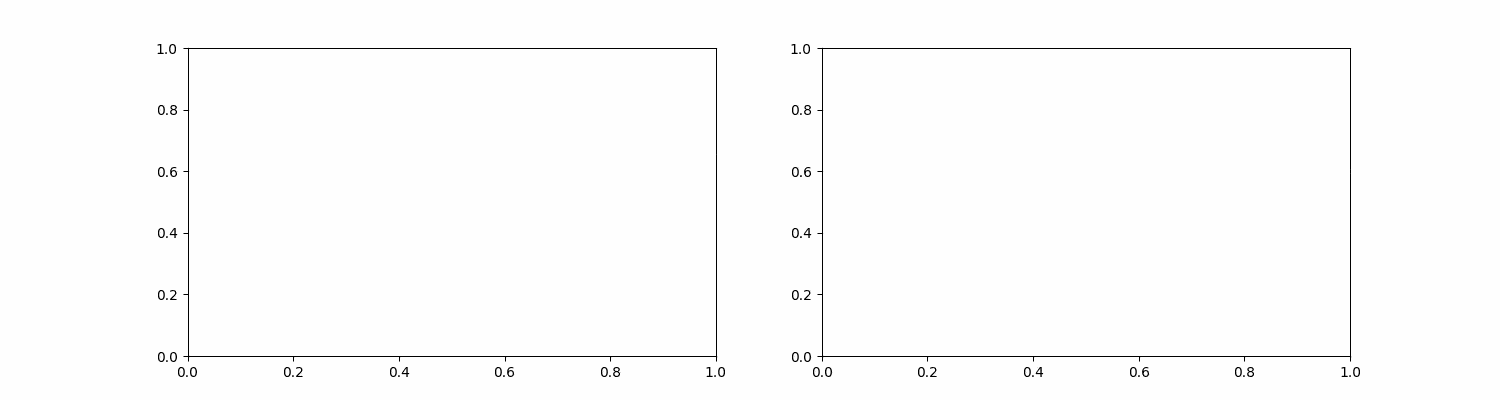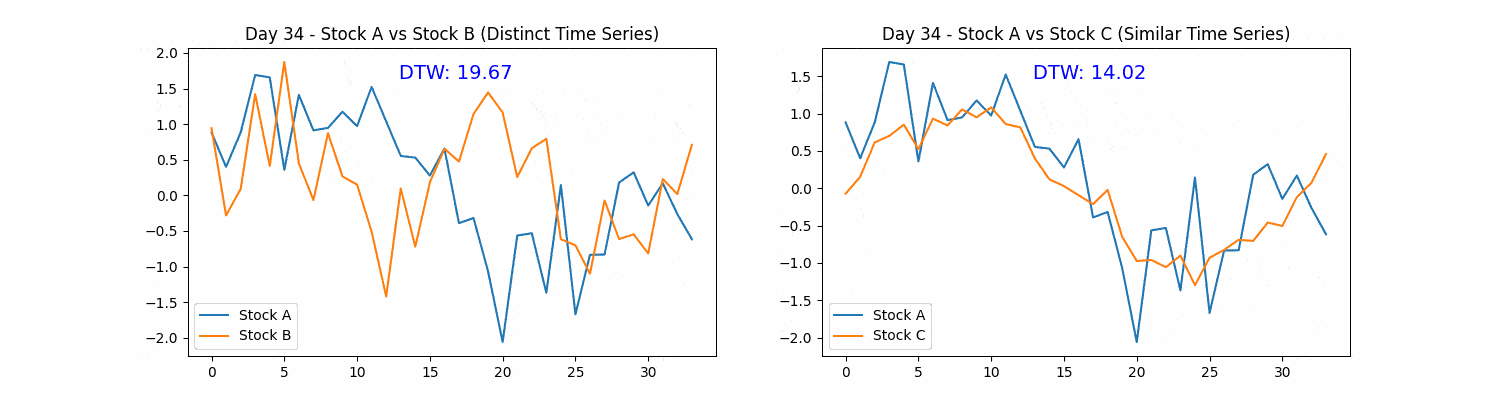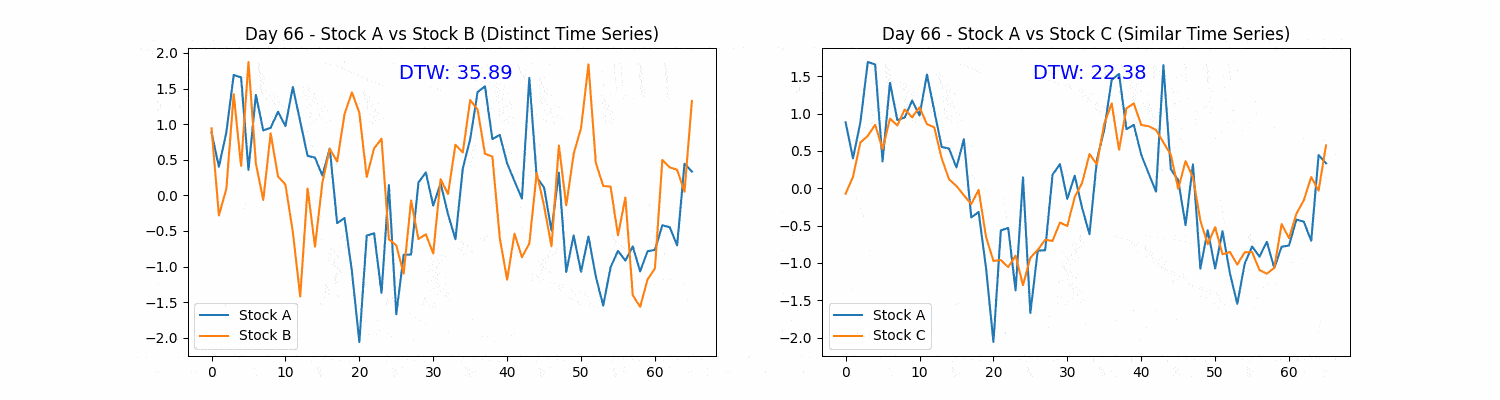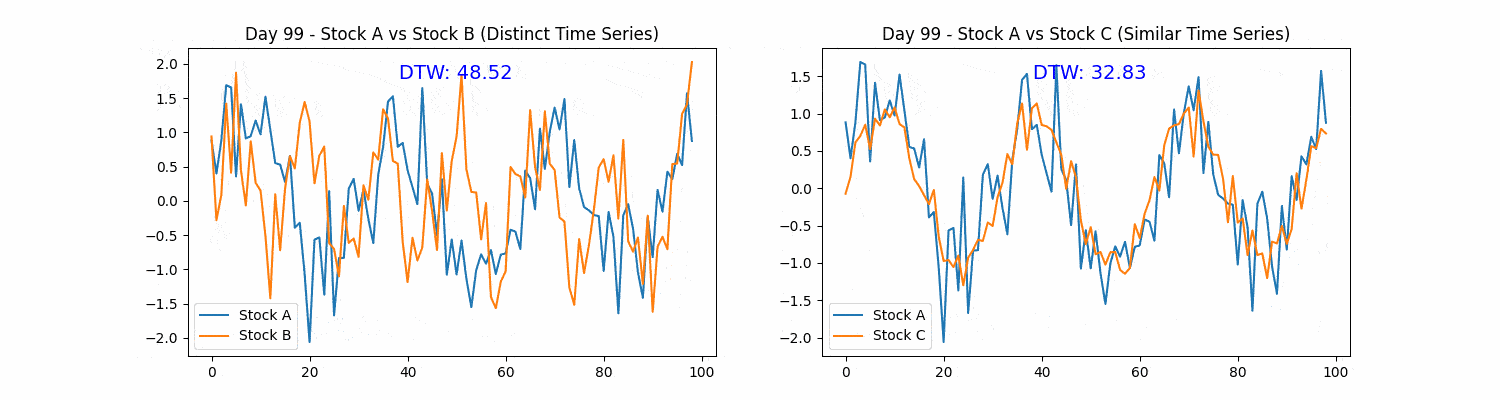
Figure. 1: Dynamic Time Warping (DTW) in Stock Analysis: The animation demonstrates two scenarios of stock price patterns, revealing divergent and parallel trends in the left and right subplots respectively. DTW distances quantify the temporal similarity between the evolving patterns, with lower DTW values indicating higher similarity, providing insights into the adaptability and precision of DTW in identifying similarities amidst temporal displacements in financial data.
2. Finding Patterns using Python
We now explore the Python implementation of DTW, focusing on pattern mining in stock prices. Our goal is to identify historical patterns that closely align with recent price movements. Let’s break it down step by step.
2.1. Normalization of Time Series Data
In time series analysis, data normalization is essential, particularly when dealing with stock prices.
It ensures a consistent scale across different price magnitudes, making comparisons more meaningful.
We define a function, normalize(ts), to transform a time series, ts. This function ensures its values are bound between 0 and 1.
def normalize(ts):
return (ts - ts.min()) / (ts.max() - ts.min())
2.2. Calculating DTW Distance
Next, the DTW distance between two time series is calculated using the dtw_distance(ts1, ts2) function, which takes two time series, ts1 and ts2, normalizes them, and computes the DTW distance by utilizing the fastdtw method from the ‘FastDTW’ library. This function will return a single scalar value representing the “distance” or dissimilarity between the two input time series.
def dtw_distance(ts1, ts2):
ts1_normalized = normalize(ts1)
ts2_normalized = normalize(ts2)
distance, _ = fastdtw(ts1_normalized.reshape(-1, 1), ts2_normalized.reshape(-1, 1), dist=euclidean)
return distance
2.3. Identifying Similar Patterns
The find_most_similar_pattern(n_days) function is designed to locate patterns within historical data. It focuses on matching a given window of n_days in the recent price movements.
This function sifts through historical price data. It compares each possible window of n_days with the recent window using DTW distance.
The five patterns with the smallest DTW distances are identified as the most similar. These patterns are then returned by the function for visualization.
def find_most_similar_pattern(n_days):
current_window = price_data_pct_change[-n_days:].values
# Adjust to find and store 5 patterns
min_distances = [(float('inf'), -1) for _ in range(5)]
for start_index in range(len(price_data_pct_change) - 2 * n_days - subsequent_days):
past_window = price_data_pct_change[start_index:start_index + n_days].values
distance = dtw_distance(current_window, past_window)
for i, (min_distance, _) in enumerate(min_distances):
if distance < min_distance:
min_distances[i] = (distance, start_index)
break
return min_distances
2.4. Visualization
Using matplotlib, we plot the overall stock price and the identified similar patterns on the same graph. This provides a clear comparative analysis of historical and recent stock price movements.
Furthermore, we reindex the identified patterns. They are plotted alongside the recent window to visually showcase their similarities, despite potential variations in magnitude. This visual comparison aids in pattern mining, highlighting how past trends align with current prices.
2.5. Data Acquisition and Preprocessing
Using yfinance, we fetch historical stock prices and calculate daily returns. We compute percentage changes to effectively navigate through fluctuations. This forms a foundation for comparative analysis using DTW.
# Get data from yfinance
ticker = "ASML.AS"
start_date = '2000-01-01'
end_date = '2023-07-21'
data = yf.download(ticker, start=start_date, end=end_date)
# Transform price data into returns
price_data = data['Close']
price_data_pct_change = price_data.pct_change().dropna()
2.6. Pattern Discovery and Analysis
First, we loop through specified windows of days to identify similar patterns. Next, we visualize these patterns alongside the recent window of price movements. This approach provides an insightful visualization of potential future price developments. By doing so, we actively engage in pattern mining based on historical data.
With this understanding in mind, let’s introduce the complete code below. Here, we combine these individual components to create a comprehensive tool. This tool is designed for identifying historical patterns in current stock price movements.
Mining Patterns In Stocks With PCA And DTW

Newsletter
One thought on “Pattern Mining for Stock Prediction with Dynamic Time Warping”