Automating Currency Arbitrage
2. Theoretical Rates vs Actual Rates
In triangular currency arbitrage, traders compare theoretical exchange rates with actual market rates to identify profitable opportunities. Theoretical rates are calculated based on two intermediary currency pairs. For example, given three currencies A, B, and C, if we want to trade from A to B through C, the theoretical rate for A/B can be derived as:
Here, Rate(A/C) is the exchange rate from currency A to C, and Rate(C/B) is the exchange rate from C to B.
The difference between this theoretical rate and the actual market rate for A/B is called the “spread.” The spread is crucial in triangular currency arbitrage as it highlights potential arbitrage opportunities. The spread is calculated as:
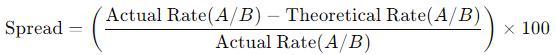
A positive spread indicates that the actual rate is higher than the theoretical rate, presenting an opportunity to sell the overpriced currency pair. A negative spread suggests buying the undervalued pair.
Additional Aspects:
No-Arbitrage Condition: In an efficient market, the theoretical and actual rates should converge, meaning the spread should be zero. This is known as the “no-arbitrage condition”, which asserts that under normal circumstances, arbitrage opportunities should not persist due to market efficiency. If the spread deviates from zero, traders act to exploit the difference, and their trades push the prices back to equilibrium.
- Transaction Costs: While the theoretical model assumes no transaction costs, real-world trading involves fees, such as spreads charged by brokers, slippage, and execution costs. Transaction costs can erode potential arbitrage profits. Therefore, traders need to account for these costs when identifying opportunities.
Liquidity Constraints: High liquidity is essential for executing triangular arbitrage trades. Low liquidity in any of the intermediary currency pairs may result in slippage, where trades are executed at a worse price than expected. This can reduce or eliminate the profit from arbitrage.
Timing of Arbitrage: Currency markets are highly volatile, and exchange rates fluctuate rapidly. Successful arbitrage requires fast execution, often achieved through automated trading systems. Timing mismatches between trades in different currency pairs can introduce risk, known as “execution risk.
3. Python Implementation
In this section, we walk through a Python implementation that calculates theoretical rates, identifies all possible arbitrage opportunities based on spread percentages, and tracks cumulative profits of the overall strategy.
3.1 Collect Historical Rate Combinations
The first step is to gather historical exchange rates for relevant currency pairs. Using the yfinance library, we can easily download exchange rate data. The code below collects historical exchange rates for a list of currencies.
The function creates a dictionary of exchange rates for every possible currency pair and stores them in a pandas DataFrame. Notably, the function handles missing data and inverses the rates when necessary, which is needed in cases where direct exchange rate data might be unavailable.
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
def collect_exchange_rates(currencies, start_date, end_date):
"""
Collects historical exchange rates for all currency pairs among the given currencies.
The function takes a list of currency codes and retrieves the exchange rates for all
possible pairs over a specified date range using the Yahoo Financ.
It first tries to download the direct exchange rate (e.g., 'USD/EUR').
If that data is unavailable, it downloads the inverse rate (e.g., 'EUR/USD') and computes
the reciprocal exchange rate.
The exchange rates are stored in a dictionary, where the keys are currency pairs and
the values are pandas Series of exchange rates indexed by date. This dictionary is
then converted into a pandas DataFrame for easier analysis.
Parameters:
- currencies (list): List of currency codes (e.g., ['USD', 'EUR', 'GBP']).
- start_date (str): Start date for the data collection in 'YYYY-MM-DD' format.
- end_date (str): End date for the data collection in 'YYYY-MM-DD' format.
Returns:
- exchange_rates_df (pd.DataFrame): A DataFrame of exchange rates with currency
pairs as columns and dates as the index.
Example:
- currencies = ['USD', 'EUR', 'JPY']
- start_date = '2020-01-01'
- end_date = '2023-01-01'
- exchange_rates_df = collect_exchange_rates(currencies, start_date, end_date)
"""
# Initialize an empty dictionary to store the exchange rate data for each currency pair
exchange_rates = {}
# Loop through all combinations of currencies (c1/c2)
for c1 in currencies:
for c2 in currencies:
if c1 == c2: # Skip if the two currencies are the same
continue
# Define the currency pair and its inverse (for fallback in case data is unavailable)
pair = f'{c1}{c2}=X'
inverse_pair = f'{c2}{c1}=X'
# Attempt to download the direct exchange rate from Yahoo Finance
data = yf.download(pair, start=start_date, end=end_date)['Adj Close']
# If the data is not available, try downloading the inverse rate
if data.empty:
data_inv = yf.download(inverse_pair, start=start_date, end=end_date)['Adj Close']
# If the inverse rate is also unavailable, skip this pair and print a message
if data_inv.empty:
print(f"Exchange rate data for {c1}/{c2} not available.")
continue
else:
# If the inverse rate is available, compute the direct rate as 1 / inverse rate
data = 1 / data_inv
data.name = f'{c1}/{c2}' # Rename the series with the proper currency pair
exchange_rates[f'{c1}/{c2}'] = data # Store in the dictionary
else:
# If the direct rate is available, store it in the dictionary
data.name = f'{c1}/{c2}'
exchange_rates[f'{c1}/{c2}'] = data
# Convert the dictionary of exchange rates into a pandas DataFrame
exchange_rates_df = pd.DataFrame(exchange_rates)
# Return the DataFrame containing all collected exchange rate data
return exchange_rates_df
3.2 Calculate Theoretical Rates
Once we have the historical data, the next step is to compute the theoretical rates. These rates are derived by calculating two-step paths between three currencies, as discussed in Section 2.
This function loops through all currency combinations and calculates the theoretical exchange rate using the two intermediary rates. Importantly, by considering all potential intermediary currencies, we ensure that the most efficient arbitrage path is used.
Also worth reading:

Newsletter