End-to-end Implementation with buy and sell signals. Indicators include Keltner Channels, Relative Volatility Index, and more
Understanding volatility is crucial in the financial markets. It not only signals potential risks but also opens up opportunities for savvy traders. This article dives into the world of volatility indicators, essential tools in any trader’s arsenal, and demonstrates their implementation in Python.
We’ll cover key indicators such as Average True Range (ATR), Bollinger Bands, Donchian Channels, Keltner Channels, Volatility Chaikin, and the Relative Volatility Index (RVI). Each offers unique insights into market dynamics, and we’ll explore their practical applications and limitations.
The indicators discussed and implemented are the following:
- Average True Range (ATR)
- Bollinger Bands
- Donchian Channels
- Keltner Channels
- Volatility Chaikin
- Relative Volatility Index (RVI)
2. Python Implementation
2.1 Average True Range (ATR)
The ATR quantifies market volatility by averaging the range of price movements. A high ATR indicates increased market volatility, often seen during market peaks, bottoms, or breakout periods.
ATR is commonly used to set stop-loss orders. For example, a trader might set a stop-loss order at a point 1.5 times the ATR below the current price to accommodate volatility.
It’s also used in trend-following strategies, where an increasing ATR might reinforce the strength of a trend. The ATR formula is given by:
Equation 1. Average True Range (ATR) formula calculates market volatility by averaging the true ranges over n periods.
n is the number of periods used for the moving average,
TRi is the true range for period i, which is the maximum of the following:
- The difference between the high and low of the current period,
- The difference between the previous close and the current high,
- The difference between the previous close and the current low.
A high ATR indicates increased market volatility, often seen during market peaks, bottoms, or breakout periods.
An insightful aspect of using the Average True Range (ATR) that may not be immediately obvious is its adaptive nature in risk management and position sizing strategies.
Unlike fixed-dollar or percentage-based stop losses, ATR allows traders to adjust their risk management thresholds based on market volatility.
This means that during periods of high volatility, stop-loss orders will be set farther away from the current price to avoid being prematurely stopped out by normal market fluctuations.
Furthermore, ATR can be instrumental in position sizing. By determining how much the market can potentially move against a position, traders can adjust the size of their positions according to the current volatility.
import yfinance as yf
import matplotlib.pyplot as plt
import pandas as pd
# Function to calculate the Average True Range (ATR)
def calculate_atr(data, window=14):
high_low = data['High'] - data['Low']
high_close = abs(data['High'] - data['Close'].shift())
low_close = abs(data['Low'] - data['Close'].shift())
ranges = pd.concat([high_low, high_close, low_close], axis=1)
true_range = ranges.max(axis=1)
atr = true_range.rolling(window=window).mean()
return atr
# Retrieve data
ticker = 'AAPL' # Example ticker
data = yf.download(ticker, start="2020-01-01", end="2023-01-01")
# Calculate ATR and its moving average
data['ATR'] = calculate_atr(data)
data['ATR_MA'] = data['ATR'].rolling(window=14).mean() # 14-day moving average of ATR
# Define buy and sell signals
buy_signal = (data['ATR'] > data['ATR_MA']) & (data['ATR'].shift(1) <= data['ATR_MA'].shift(1))
sell_signal = (data['ATR'] < data['ATR_MA']) & (data['ATR'].shift(1) >= data['ATR_MA'].shift(1))
# Plotting
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(25, 8), sharex=True) # Share x-axis
# Stock price plot with ATR-based buy and sell signals
ax1.plot(data['Close'], label='Close Price', alpha=0.5)
ax1.scatter(data.index[buy_signal], data['Close'][buy_signal], label='Buy Signal (ATR)', marker='^', color='green', alpha=1)
ax1.scatter(data.index[sell_signal], data['Close'][sell_signal], label='Sell Signal (ATR)', marker='v', color='red', alpha=1)
for idx in data.index[buy_signal]:
ax1.axvline(x=idx, color='green', linestyle='--', alpha=0.5)
for idx in data.index[sell_signal]:
ax1.axvline(x=idx, color='red', linestyle='--', alpha=0.5)
ax1.set_title(f'{ticker} Stock Price with ATR-Based Signals')
ax1.set_ylabel('Price')
ax1.legend()
# ATR subplot with buy and sell signals
ax2.plot(data['ATR'], label='Average True Range', color='purple')
ax2.plot(data['ATR_MA'], label='14-day MA of ATR', color='orange', alpha=0.6)
ax2.scatter(data.index[buy_signal], data['ATR'][buy_signal], label='Buy Signal (ATR)', marker='^', color='green')
ax2.scatter(data.index[sell_signal], data['ATR'][sell_signal], label='Sell Signal (ATR)', marker='v', color='red')
for idx in data.index[buy_signal]:
ax2.axvline(x=idx, color='green', linestyle='--', alpha=0.5)
for idx in data.index[sell_signal]:
ax2.axvline(x=idx, color='red', linestyle='--', alpha=0.5)
ax2.set_title(f'{ticker} Average True Range (ATR) with Signals')
ax2.set_ylabel('ATR')
ax2.legend()
plt.tight_layout()
plt.show()
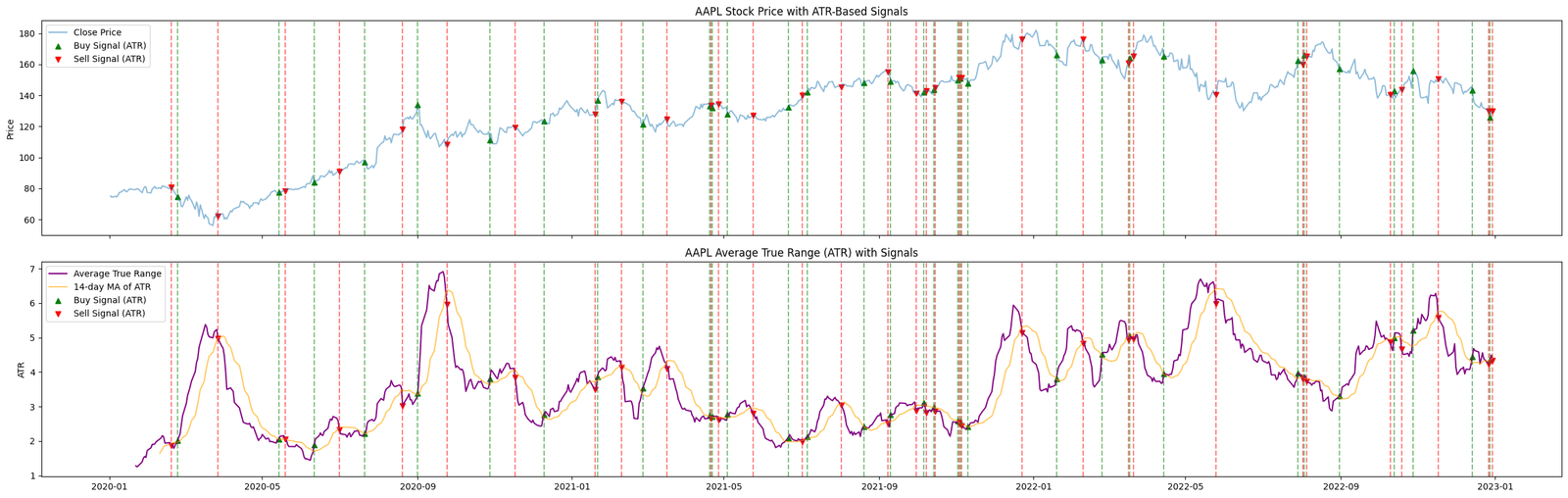
Figure. 1: Stock price with ATR-based buy (green) and sell (red) signals, and the ATR value with its 14-day moving average.
2.2 Bollinger Bands
These bands provide insights into market volatility and overbought/oversold conditions. Bollinger bands for sure among the top volatility indicators. Bollinger Bands are used for mean-reversion strategies; buying when the price hits the lower band and selling when it hits the upper band.
- Middle Band (MB): The simple moving average (SMA) of the last n periods. MB=SMA(n)
- Upper Band (UB): Set k standard deviations (SD) above the middle band. UB=MB+(k×SD)
- Lower Band (LB): Set k standard deviations (SD) below the middle band. LB=MB−(k×SD)
Bands widening indicate increased market volatility, and narrowing bands suggest decreased volatility.
An insightful, yet less immediately obvious aspect of Bollinger Bands is their ability to adjust to market conditions dynamically, similar to ATR for volatility.
However, Bollinger Bands add a layer of trend analysis by visually representing the price relative to its recent range. When the bands tighten (“squeeze”), it often precedes a significant price move in either direction, indicating that the market is consolidating and a breakout is imminent.
import yfinance as yf
import matplotlib.pyplot as plt
import pandas as pd
def calculate_bollinger_bands(data, window=20, num_of_std=2):
rolling_mean = data['Close'].rolling(window=window).mean()
rolling_std = data['Close'].rolling(window=window).std()
upper_band = rolling_mean + (rolling_std*num_of_std)
lower_band = rolling_mean - (rolling_std*num_of_std)
return rolling_mean, upper_band, lower_band
# Retrieve data
ticker = 'AAPL' # Example ticker
data = yf.download(ticker, start="2020-01-01", end="2023-01-01")
# Calculate Bollinger Bands
data['Middle Band'], data['Upper Band'], data['Lower Band'] = calculate_bollinger_bands(data)
# Define buy and sell signals
buy_signal = (data['Close'] < data['Lower Band']) & (data['Close'].shift(1) >= data['Lower Band'].shift(1))
sell_signal = (data['Close'] > data['Upper Band']) & (data['Close'].shift(1) <= data['Upper Band'].shift(1))
# Plotting
fig, ax = plt.subplots(figsize=(25, 8))
# Stock price plot with Bollinger Bands and buy/sell signals
ax.plot(data['Close'], label='Close Price', alpha=1, linewidth=2)
ax.plot(data['Middle Band'], label='Middle Band (20-day SMA)', color='blue', alpha=0.5)
ax.plot(data['Upper Band'], label='Upper Band (2 Std Dev)', color='red', alpha=0.5)
ax.plot(data['Lower Band'], label='Lower Band (2 Std Dev)', color='green', alpha=0.5)
ax.fill_between(data.index, data['Lower Band'], data['Upper Band'], color='grey', alpha=0.1)
ax.scatter(data.index[buy_signal], data['Close'][buy_signal], label='Buy Signal', marker='^', color='green', alpha=1)
ax.scatter(data.index[sell_signal], data['Close'][sell_signal], label='Sell Signal', marker='v', color='red', alpha=1)
ax.set_title(f'{ticker} Stock Price with Bollinger Bands')
ax.set_ylabel('Price')
ax.legend()
plt.tight_layout()
plt.show()
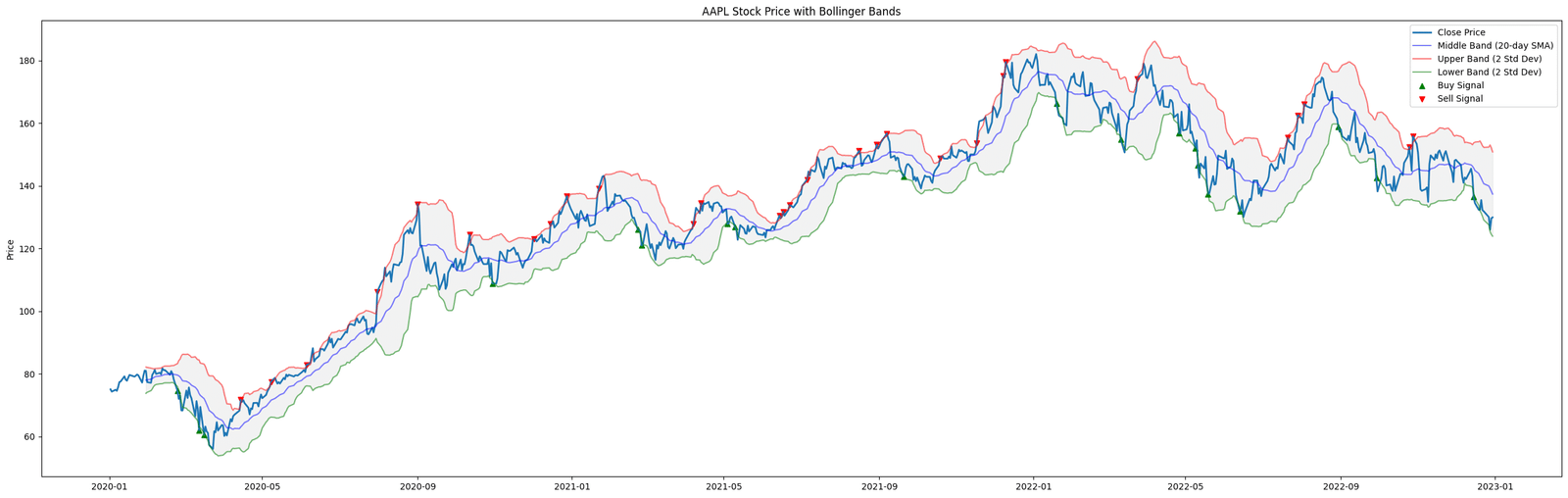
Figure. 2: Stock price movement within Bollinger Bands, marking buy signals when the price touches the Lower Band and sell signals at the Upper Band. The bands' expansion and contraction visually represent market volatility.
2.3 Donchian Channels
These channels are based on the highest high and lowest low, offering a view of market range and volatility. The width of the channel reflects volatility; wider channels suggest more volatility. Donchian Channels are popular in breakout strategies.
A buy signal is generated when the price breaks above the upper band and a sell signal when it breaks below the lower band. These channels also help in trend following, where the price staying above or below a channel can indicate a strong trend.
- Upper Band (UB): max(High over last n periods)
- Lower Band (LB): min(Low over last n periods)
A nuanced aspect of Donchian Channels is their efficacy in highlighting consolidation phases within the market. When the channels narrow, it signifies a decrease in volatility, indicating that the asset is consolidating. This can be particularly insightful for traders looking for breakout opportunities, as periods of consolidation often precede significant price movements.
import yfinance as yf
import matplotlib.pyplot as plt
import pandas as pd
def calculate_donchian_channel(data, window=20):
data['Upper'] = data['High'].rolling(window=window).max()
data['Lower'] = data['Low'].rolling(window=window).min()
data['Middle'] = (data['Upper'] + data['Lower']) / 2
return data
def generate_signals(data):
# Buy when the close price crosses above the upper band from below
buy_signals = (data['Close'] < data['Lower'].shift(1)) & (data['Close'].shift(1) >= data['Lower'].shift(1))
# Sell when the close price crosses below the lower band from above
sell_signals = (data['Close'] > data['Upper'].shift(1)) & (data['Close'].shift(1) <= data['Upper'].shift(1))
return buy_signals, sell_signals
# Retrieve data
ticker = 'AAPL' # Example ticker
data = yf.download(ticker, start="2020-01-01", end="2023-01-01")
# Calculate Donchian Channels with 20-day period
window = 60
data = calculate_donchian_channel(data, window)
# Generate buy and sell signals
buy_signals, sell_signals = generate_signals(data)
data['Buy Signals'] = buy_signals
data['Sell Signals'] = sell_signals
# Plotting
fig, ax = plt.subplots(figsize=(25, 8))
# Stock price plot with Donchian Channels and buy/sell signals
ax.plot(data['Close'], label='Close Price', alpha=0.5)
ax.plot(data['Upper'], label='Upper Donchian Channel', linestyle='--', alpha=0.4)
ax.plot(data['Lower'], label='Lower Donchian Channel', linestyle='--', alpha=0.4)
ax.plot(data['Middle'], label='Middle Donchian Channel', linestyle='--', alpha=0.4)
ax.fill_between(data.index, data['Lower'], data['Upper'], color='grey', alpha=0.1)
# Mark buy and sell signals
ax.scatter(data.index[data['Buy Signals']], data['Close'][data['Buy Signals']], label='Buy Signal', marker='^', color='green', alpha=1)
ax.scatter(data.index[data['Sell Signals']], data['Close'][data['Sell Signals']], label='Sell Signal', marker='v', color='red', alpha=1)
ax.set_title(f'{ticker} Stock Price with Donchian Channels')
ax.set_ylabel('Price')
ax.legend()
plt.tight_layout()
plt.show()
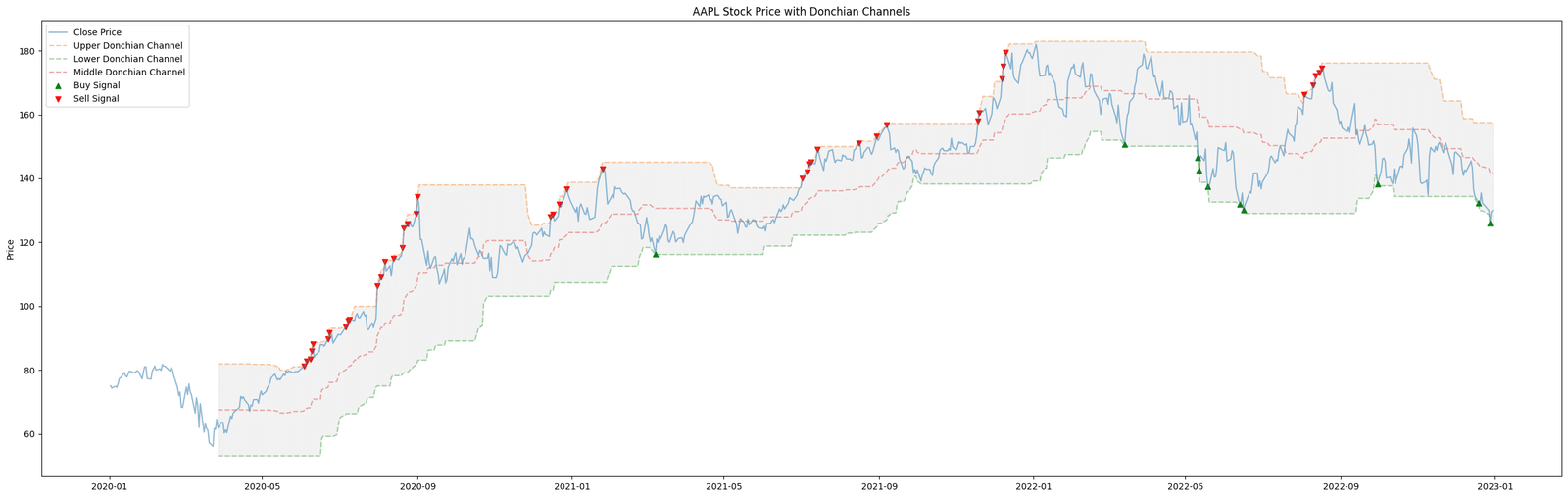
Figure. 3: Stock Price movement with Donchian Channels, highlighting buy signals with green markers when the price exceeds the Upper Band and sell signals with red markers when falling below the Lower Band.
2.4 Keltner Channels
Keltner Channels use ATR for band setting, making them sensitive to volatility spikes. The channels expand in more volatile markets and contract in calmer markets.
Similar to Bollinger Bands, they can be used for mean-reversion and breakout strategies. A common approach is to buy when the price closes back inside the channel after going outside, indicating a potential reversal
- Middle Line (ML): Exponential moving average (EMA) of the last n periods. ML=EMA(n)
- Upper Band (UB): ML plus k times the Average True Range (ATR). UB=ML+(k×ATR)
- Lower Band (LB): ML minus k times the ATR. LB=ML−(k×ATR)
Keltner Channels provide a unique insight into market trends by integrating the concept of volatility with the Exponential Moving Average (EMA).
A critical observation not immediately obvious is that while Keltner Channels and Bollinger Bands might look similar in representing volatility, Keltner Channels’ use of ATR for band setting offers a more consistent measure of volatility due to ATR’s focus on price movement extremes.
This makes Keltner Channels particularly useful in distinguishing between normal price fluctuations and significant price moves, offering traders a clearer signal for potential breakouts or reversals based on volatility and price trends, not just price action relative to a moving average.
Related Articles
Identify Key Market Shifts With The Volatility Ratio

Newsletter