A Comprehensive Guide for Automating IV Analysis in Python
Implied Volatility (IV) shows the market’s expectations of future price movements for an underlying asset. This article will show you how to automate Implied Volatility Analysis using Python. By following this guide, you will learn how to gather options data, plot volatility smiles, and interpret key metrics like open interest and the Greeks.
In this guide, we provide complete Python code snippets and step-by-step instructions to streamline the analysis process. Additionally, we offer an end-to-end implementation in Python and Google Colab. For non-coding users, a user-friendly tool is available to conduct similar investigation without coding to determine market sentiment on future prices.
This article covers the following:
- Understanding IV
- Gathering Options Data
- Volatility Smile Analysis
- Open Interest Analysis
- Volume in Option Prices
- Volatility Surface Plot
- Historical IV Analysis
- Sentiment Analysis
1. Implied Volatility as a Tool
Unlike historical volatility, which looks at past price movements, IV is forward-looking. It provides insights into how much the market expects the price of an asset to move in the future.
Traders rely on Implied Volatility Analysis to gauge market sentiment and price options accurately. When IV is high, it suggests that the market expects significant price changes. Conversely, low IV indicates that traders anticipate stable prices. This expectation affects options premiums: higher IV leads to higher premiums, while lower IV results in cheaper options.
The formula for IV is derived from the Black-Scholes model. While the Black-Scholes formula itself is used to price options, IV is the value that, when input into the model, results in a theoretical option price equal to the current market price.
To solve for IV, we can use iterative numerical methods since there’s no closed-form solution. This involves adjusting σ until the calculated option price matches the market price.
Market Sentiment
Implied volatility reveals market sentiment. For example, during earnings season, IV often rises as traders anticipate significant price swings based on earnings reports.
If a company’s earnings are approaching, and IV spikes, traders expect volatility. This anticipation allows traders to adjust their positions. They might buy options to capitalize on expected price movements or sell options to benefit from higher premiums.
Option Pricing
IV directly influences option prices. Consider a tech stock during a product launch. If IV increases, the option premiums rise because the market expects larger price movements.
A trader selling options in this period benefits from higher premiums. Conversely, if IV is low, like during a calm market phase, buying options is cheaper. If you expect future volatility, purchasing options now can be cost-effective.
Volatility Smiles and Surfaces
Visual representations like volatility smiles help traders understand IV variations. For instance, if you plot IV against strike prices and notice a U-shaped curve (volatility smile), it indicates higher IV for in-the-money and out-of-the-money options.
This pattern is common during market stress, suggesting traders expect significant movements at extreme prices. A trader seeing this might avoid selling options at these extremes due to high risk.
Open Interest and Volume Analysis
Monitoring open interest and trading volume alongside IV offers insights into market activity. Suppose a stock shows high open interest and volume in call options with rising IV.
The above indicates bullish sentiment, as many traders are betting on price increases. Knowing this, a trader might decide to go long on the stock or buy call options to align with the market sentiment.
The Greeks
The Greeks help manage risk and reward in options trading.
- Delta: If you hold a call option with a delta of 0.6, for every $1 increase in the stock price, the option price increases by $0.60. This helps in hedging positions.
- Gamma: If a call option has high gamma, a small price movement in the underlying stock significantly changes the delta, indicating potential for large gains or losses.
- Theta: For options nearing expiration, theta is vital. If you own a call option with high theta, it loses value quickly as time passes. This decay must be managed in time-sensitive strategies.
- Vega: A high vega option is very sensitive to volatility changes. In a market expecting big news, such as a regulatory decision, traders might choose high vega options to benefit from increased volatility.
Historical IV Comparison
Comparing current IV with historical levels helps gauge option value. Suppose a stock’s current IV is much higher than its historical average. This might indicate market overreaction or heightened fear, suggesting an opportunity to sell options at a premium. Conversely, if current IV is lower, it might be a good time to buy options cheaply, expecting future volatility to rise.
2. Gathering Options Data
yfinance to fetch the latest options data and pandas for data manipulation. It’s important to note that the data retrieved will reflect the most current options available and no historical data is available at this point.- contractSymbol: Unique identifier for the options contract.
- lastTradeDate: Date and time of the last trade for the option.
- strike: Strike price of the option.
- lastPrice: Last traded price of the option.
- bid: Current bid price.
- ask: Current ask price.
- change: Change in price from the previous close.
- percentChange: Percentage change in price from the previous close.
- volume: Number of contracts traded during the last trading session.
- openInterest: Total number of outstanding contracts.
- impliedVolatility: The implied volatility of the option, stated in the data.
- inTheMoney: Indicates whether the option is in the money.
- expiration: Expiration date of the option.
- type: Type of option (call or put).
import yfinance as yf # Import yfinance for financial data
import pandas as pd # Import pandas for data manipulation
ticker = "ASML" # Example ticker
def get_options_data(ticker):
asset = yf.Ticker(ticker) # Create a Ticker object for the specified ticker
exp_dates = asset.options # Get available expiration dates for options
if not exp_dates: # Check if there are no expiration dates available
print(f"No options data available for ticker {ticker}.")
return None, None
recent_price = asset.history(period="1d")["Close"].iloc[-1] # Get the most recent closing price
options_data = [] # Initialize an empty list to hold options data
for date in exp_dates: # Loop through each expiration date
calls = asset.option_chain(date).calls # Get call options data for the date
puts = asset.option_chain(date).puts # Get put options data for the date
calls["expiration"] = date # Add expiration date to calls data
puts["expiration"] = date # Add expiration date to puts data
calls["type"] = "call" # Add option type to calls data
puts["type"] = "put" # Add option type to puts data
data = pd.concat([calls, puts]) # Concatenate calls and puts data
options_data.append(data) # Append the data to the options_data list
if not options_data: # Check if there is no valid options data
print(f"No valid options data available for ticker {ticker}.")
return None, None
options_data = pd.concat(options_data) # Concatenate all options data into a single DataFrame
options_data = options_data[options_data["strike"].between(recent_price * 0.9, recent_price * 1.1)] # Filter data to include strikes within 10% of the recent price
options_data["implied_volatility"] = options_data["impliedVolatility"] * 100 # Convert implied volatility to percentage
return options_data, recent_price # Return the options data and recent price
options_data, recent_price = get_options_data(ticker) # Get options data for the specified ticker
options_data # Display the options data
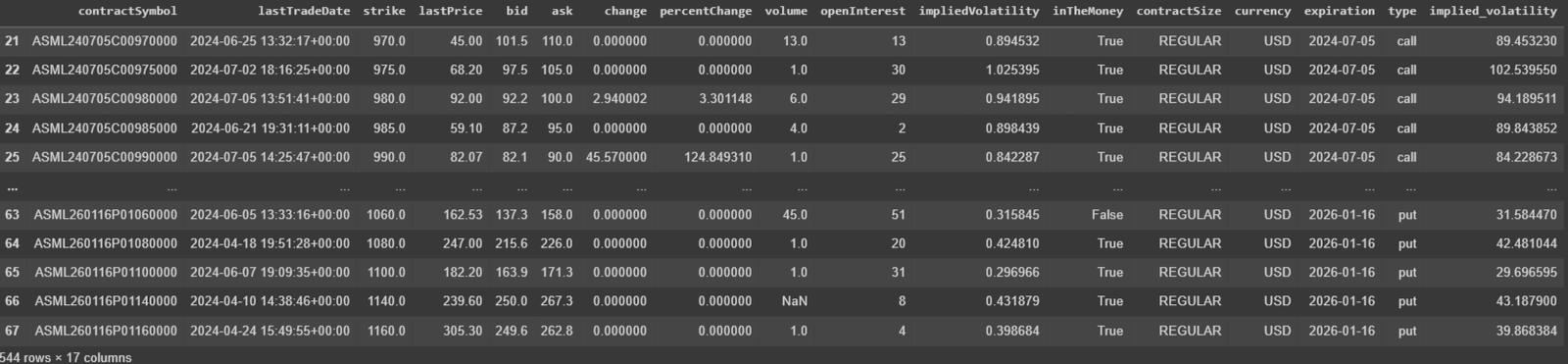
Figure. 1: Sample of the Latest ASML Options Data Including Implied Volatility and Open Interest.
3. Volatility Smile
As previously mentioned, a Volatility Smile is a graphical representation of IV across different strike prices for options with the same expiration date. It provides insights into market expectations and sentiment.
Typically, a “smile” shape forms because out-of-the-money (OTM) and in-the-money (ITM) options tend to have higher IVs than at-the-money (ATM) options. This reflects increased risk perception and demand for protection against significant price changes.
The Volatility Smile phenomenon highlights a flaw in the Black-Scholes Model (BSM). The BSM assumes that IV is constant across all strike prices and expiration dates. However, real market data shows that this is not true.
The smile shape occurs because market participants adjust their volatility expectations based on perceived risks and supply-demand dynamics for different strike prices.
Why the Volatility Smile Occurs:
Market Risks and Events: Traders often expect significant price movements due to upcoming events or inherent risks in the underlying asset. This expectation leads to higher IV for options that are far from the current market price, either deep in-the-money or out-of-the-money.
Demand and Supply Dynamics: The demand for OTM options, often used for hedging or speculation, can drive up their IV. Similarly, ITM options may have higher IV due to the higher premium and risk associated with these options.
Leverage and Hedging: Market participants use OTM options for leverage, which means they require less capital to control the same amount of underlying asset. This increased usage can raise the IV. Similarly, institutions may use ITM options for hedging large positions, driving up their IV.
Behavioral Factors: Traders’ psychological factors and biases also contribute to the Volatility Smile. For example, the fear of large market moves can lead to higher demand for protective puts, increasing their IV.
import plotly.graph_objects as go # Import Plotly for graph objects
from plotly.subplots import make_subplots # Import Plotly for creating subplots
def plot_volatility_smile(options_data, recent_price, ticker):
if options_data is not None: # Check if options data is available
calls_data = options_data[options_data["type"] == "call"] # Filter for call options
puts_data = options_data[options_data["type"] == "put"] # Filter for put options
expirations = options_data['expiration'].unique() # Get unique expiration dates
color_map_2d = px.colors.qualitative.Prism # Define a color map for plotting
fig = make_subplots(rows=1, cols=2, subplot_titles=["Calls", "Puts"], shared_yaxes=True) # Create subplots for calls and puts
for exp, color in zip(expirations, color_map_2d): # Loop through expiration dates and colors
exp_calls = calls_data[calls_data["expiration"] == exp] # Filter call options by expiration date
exp_puts = puts_data[puts_data["expiration"] == exp] # Filter put options by expiration date
fig.add_trace(go.Scatter(x=exp_calls["strike"], y=exp_calls["implied_volatility"], mode='markers',
marker=dict(color=color), name=exp), row=1, col=1) # Plot call options
fig.add_trace(go.Scatter(x=exp_puts["strike"], y=exp_puts["implied_volatility"], mode='markers',
marker=dict(color=color), name=exp, showlegend=False), row=1, col=2) # Plot put options
avg_iv_by_strike_calls = calls_data.groupby("strike")["implied_volatility"].mean() # Calculate average IV by strike for calls
avg_iv_by_strike_puts = puts_data.groupby("strike")["implied_volatility"].mean() # Calculate average IV by strike for puts
fig.add_trace(go.Scatter(x=avg_iv_by_strike_calls.index, y=avg_iv_by_strike_calls.values, mode='lines',
line=dict(color='black', dash='dash'), name='Avg. IV by Strike (Calls)'), row=1, col=1) # Plot average IV for calls
fig.add_trace(go.Scatter(x=avg_iv_by_strike_puts.index, y=avg_iv_by_strike_puts.values, mode='lines',
line=dict(color='black', dash='dash'), name='Avg. IV by Strike (Puts)', showlegend=False), row=1, col=2) # Plot average IV for puts
overall_avg_iv_calls = calls_data["implied_volatility"].mean() # Calculate overall average IV for calls
overall_avg_iv_puts = puts_data["implied_volatility"].mean() # Calculate overall average IV for puts
fig.add_hline(y=overall_avg_iv_calls, line=dict(color='gray', dash='dash'),
annotation_text=f"Overall Avg. IV (Calls): {overall_avg_iv_calls:.2f}%",
row=1, col=1) # Add horizontal line for overall average IV of calls
fig.add_hline(y=overall_avg_iv_puts, line=dict(color='gray', dash='dash'),
annotation_text=f"Overall Avg. IV (Puts): {overall_avg_iv_puts:.2f}%",
row=1, col=2) # Add horizontal line for overall average IV of puts
fig.update_layout(title=f"{ticker} Volatility Smile - Current Price: {recent_price:.2f}", showlegend=True, legend_title_text='Expiration Date') # Update layout
fig.update_xaxes(title_text="Strike Price") # Set x-axis title
fig.update_yaxes(title_text="Implied Volatility (%)") # Set y-axis title
fig.show() # Display the plot
# Return necessary data for interpretation
return overall_avg_iv_calls, overall_avg_iv_puts, avg_iv_by_strike_calls, avg_iv_by_strike_puts, expirations
# Assuming options_data and recent_price are already defined
overall_avg_iv_calls, overall_avg_iv_puts, avg_iv_by_strike_calls, avg_iv_by_strike_puts, expirations = plot_volatility_smile(options_data, recent_price, ticker)
def interpret_volatility_smile(ticker, overall_avg_iv_calls, overall_avg_iv_puts, avg_iv_by_strike_calls, avg_iv_by_strike_puts):
# Interpretation based on data
interpretation = f"**Interpretation of {ticker} Volatility Smile:**\n"
# Average IV comparison
interpretation += f"- The average implied volatility for call options is {overall_avg_iv_calls:.2f}%.\n"
interpretation += f"- The average implied volatility for put options is {overall_avg_iv_puts:.2f}%.\n"
# Volatility smile presence
if avg_iv_by_strike_calls.var() > 0.1: # Check if variance of IV by strike for calls is significant
interpretation += "- The call options exhibit a noticeable 'volatility smile,' indicating varying implied volatility across different strike prices.\n"
else:
interpretation += "- The call options do not show a significant 'volatility smile,' suggesting more stable implied volatility across strike prices.\n"
if avg_iv_by_strike_puts.var() > 0.1: # Check if variance of IV by strike for puts is significant
interpretation += "- The put options exhibit a noticeable 'volatility smile,' indicating varying implied volatility across different strike prices.\n"
else:
interpretation += "- The put options do not show a significant 'volatility smile,' suggesting more stable implied volatility across strike prices.\n"
# Market sentiment based on IV
market_sentiment = "bullish" if overall_avg_iv_calls > overall_avg_iv_puts else "bearish"
interpretation += f"- The overall market sentiment is {market_sentiment}, inferred from the average implied volatility of calls and puts.\n"
# Conclusion based on data trends
if overall_avg_iv_calls > overall_avg_iv_puts:
interpretation += "- The higher implied volatility in call options suggests that traders expect upward price movements or higher uncertainty in the stock price.\n"
else:
interpretation += "- The higher implied volatility in put options suggests that traders expect downward price movements or higher uncertainty in the stock price.\n"
print(interpretation) # Print the interpretation
# Generate interpretation based on the results from the plot function
interpret_volatility_smile(ticker, overall_avg_iv_calls, overall_avg_iv_puts, avg_iv_by_strike_calls, avg_iv_by_strike_puts)
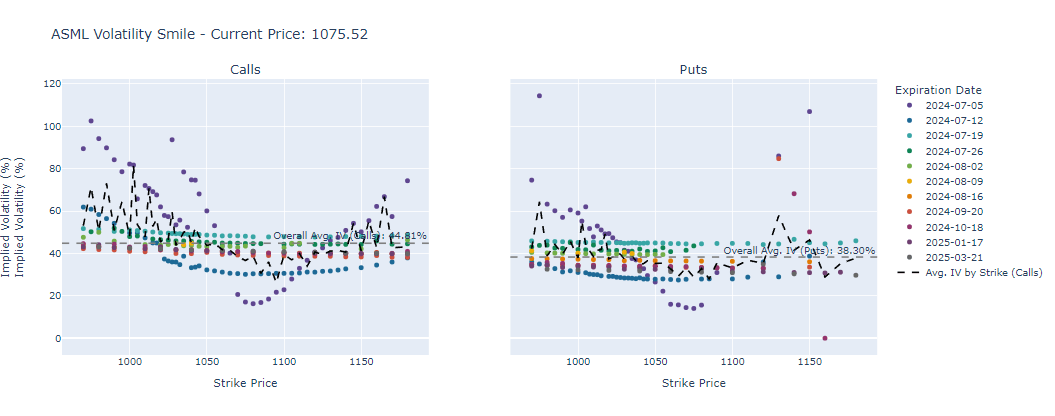
Figure. 2: Volatility Smile for ASML Options: Call and Put Implied Volatility by Strike Price.
**Interpretation of ASML Volatility Smile:**
- The average implied volatility for call options is 44.81%.
- The average implied volatility for put options is 38.30%.
- The call options exhibit a noticeable 'volatility smile,' indicating varying implied volatility across different strike prices.
- The put options exhibit a noticeable 'volatility smile,' indicating varying implied volatility across different strike prices.
- The overall market sentiment is bullish, inferred from the average implied volatility of calls and puts.
- The higher implied volatility in call options suggests that traders expect upward price movements or higher uncertainty in the stock price.
Also worth reading:
Top 6 Volatility Indicators In Python
Identify Key Market Shifts With The Volatility Ratio
Assessing Future Stock Price Movements With Historical & Implied Volatility

Newsletter