A Comprehensive Guide Fine-tune a Code LLM on Private Code using a Single GPU to Enhance its Contextual Awareness
Recently, powerful language models like Codex, StarCoder, and Code Llama that can understand and generate code have been created. These models are trained on vast code data spanning multiple programming languages. While impressive, to get the most value from them within an organization, we need to fine-tune or customize the models.
Fine-tuning allows us to adjust the model’s outputs to match an organization’s coding style guidelines. For example, aligning with internal code libraries, and best practices.
This ensures the generated code fits nicely into existing codebases and meets quality standards. However, the typical fine-tuning process requires a lot of computing power. This can be challenging for organizations without access to high-end hardware.
This tutorial demonstrates how LoRA (Low-Rank Adaptation) efficiently fine-tunes models. LoRA fine-tunes the model by training just a small number of new parameters. This tricks the model into behaving as if it was fully fine-tuned.
With LoRA, it becomes feasible to customize powerful code generation models like Codex on a single GPU. We’ll discuss how to use this LoRA technique so you can adapt these incredible AI models for your specific coding needs.
This article is structured as follows:
- Theoretical background on code LLMs
- Preparing a suitable dataset for training
- Parameter-efficient fine-tuning methodology
- Advanced optimization techniques
- incorporating fine-tuned LLMs into development workflows
1. Theoretical Background of Code LLMs
1.1 Code-Specific Transformer Architectures
Although Transformers form the basis for many LLMs, code-specific models require architectural adjustments to manage the complexities of programming languages. Let’s explore these adaptations:
1. Encoder-Decoder with Specialized Attention Mechanisms:
The foundational architecture of code LLMs often mirrors the encoder-decoder structure found in standard Transformers. The encoder captures the syntax and semantics of the input code sequence.
The decoder then generates output code, using attention mechanisms to focus on relevant parts of the encoded information. However, code-specific models incorporate specialized attention layers to address the unique sequential nature of code.
Masked Attention
Prevents information leakage during decoding. The model only attends to past tokens in the input sequence, ensuring it focuses on already generated code and doesn’t “cheat” by peeking at future code. This can be represented as:
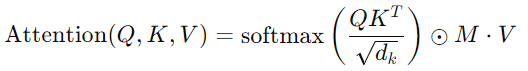
Equation 1. Formula for computing masked attention, ensuring focus only on preceding tokens in the sequence.
Where Q, K, and V are the queries, keys, and values matrices respectively, dk is the dimension of the keys, and M is a mask matrix that ensures attention is only applied to previous tokens.
Relative Positional Encoding
Captures the relative distance between code tokens, allowing the model to understand how far back or forward to look in the code sequence for relevant information. (Consider adding a brief mention of techniques like Shift Attention or Sinusoidal Encodings if appropriate for your audience’s technical level).
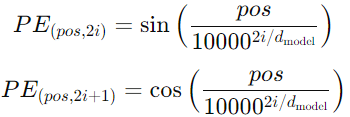
Equation 2. Sine and Cosine function for calculating relative positional encodings for even and odd indices in the embedding.
Where pos is the position and i is the dimension. This allows the model to determine the relative positions of tokens within the sequence.
Hierarchical Attention
For models handling complex code structures, hierarchical attention allows the model to focus on both local dependencies between neighboring tokens and long-range dependencies across nested code structures (e.g., loops, conditionals).
Equation 3. Combines local and global attention mechanisms, weighted by factor α, for hierarchical attention.
Where pos is the position and i is the dimension. This allows the model to determine the relative positions of tokens within the sequence.
2. Code-Aware Embeddings: Capturing Meaning Beyond Words
While word embeddings like Word2Vec or GloVe are crucial for representing code tokens, they are insufficient for code LLMs, which utilize additional embedding techniques tailored for code elements:
Function Embeddings
Capture not only the semantics of individual function names but also their relationship to other code elements. They are learned by considering the function’s definition, arguments, return type, and how it interacts with other functions in the codebase.
Function embeddings are learned through methods like lookup tables mapped to pre-trained vectors or contextual embeddings that average surrounding tokens or use RNNs to capture the function’s context.
Equation 4. Represents function embeddings as contextual combinations of function names, arguments, and returns.
This equation conceptualizes how a function’s embedding might be generated from its name, arguments, and return types through a hypothetical ContextualEmbedding process.
Variable Embeddings
Represent variables by encoding their type information (e.g., integer, string) and usage patterns within the code, going beyond simple one-hot encoding.
Variable embeddings can be learned by integrating type information and usage patterns, for example, through concatenation.
Equation 5. Combines type and usage embeddings for variables using weighted matrices.
Where hvar is the variable embedding vector, Wtype and Wusage are weight matrices for type and usage information, respectively, and type_embedding and usage_embedding are the embedding vectors representing the variable’s type and usage pattern.
3. AST-based Encoders: Unveiling Code Structure
Some code LLMs use encoders that explicitly process the Abstract Syntax Tree (AST) representation of code, capturing the hierarchical structure and revealing relationships between code elements. Graph Neural Networks (GNNs) process AST nodes and edges to enrich code representation with structural information.
GNNs aggregate information from neighboring nodes in the AST graph through message passing:x
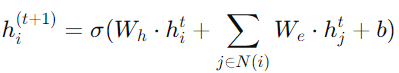
Equation 6. Updates the hidden state of AST nodes by aggregating transformed neighbor node information.
where hi(t) is the hidden state of node i at iteration t, Wh and We are weight matrices for message transformation, N(i) denotes the neighboring nodes of i, σ is an activation function, and b is a bias vector.
This process enables GNNs to learn representations that incorporate information from both the node itself and its connected nodes, capturing the hierarchical structure of the code.
1.2 Training Code LLMs
Training code LLMs involves unsupervised learning on extensive datasets compiled from public code repositories.
The model learns to predict the next token in a sequence, optimizing the weight parameters to minimize the prediction loss across the dataset.
The objective function, represented as the negative log-likelihood of predicting the next token, is given by:
Equation 7. Loss function for training, maximizing the probability of correctly predicting the next token.
where xt denotes the token at position t, x<t represents the sequence of tokens preceding t, and θ are the model parameters. Training code LLMs also entails the use of techniques such as masked language modeling described above, where random tokens are masked.
1.3 Fine-Tuning Code LLMs
Fine-tuning code LLMs on specific datasets enables the customization of these models for particular coding styles, conventions, or the use of proprietary libraries.
This process adjusts pre-trained model parameters to optimize domain-specific performance, aligning outputs with organizational needs.
The fine-tuning process is driven by a domain-specific loss function:
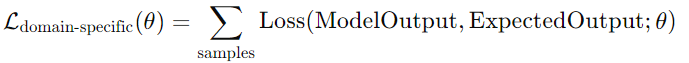
Equation 8. Calculates the loss for fine-tuning on domain-specific data, optimizing model performance for tailored outputs.
This equation tailors the pre-trained model to a specific coding domain or style.
Fine-tuning is not without challenges, particularly regarding computational resources and the risk of overfitting on specialized datasets.
Techniques such as the introduction of task-specific adapters, Low-Rank Adaptation (LoRA), and employing regularization strategies are critical to addressing these challenges.
LoRA, for instance, modifies the weight matrices in the Transformer layers through low-rank updates, enabling efficient fine-tuning by optimizing a smaller subset of parameters.
Weight Matrix Updates in LoRA
Equation 9. Represents weight matrix updates in LoRA, enabling efficient fine-tuning by optimizing a smaller subset of parameters.
Where Wbase is the original weight matrix of the Transformer layer, and U and V are smaller matrices that represent the low-rank updates, allowing for efficient fine-tuning.
This approach minimizes the computational overhead and mitigates the risk of overfitting, making fine-tuning more feasible on resource-constrained setups, such as single GPU environments.
If you want to know more about LoRA, please read the following papers:
- Parameter-Efficient Tuning of Transformers with Linear Attention (LORA): https://arxiv.org/pdf/2306.07967 by Shazeer et al. (2023).
- LoRA: Low-Rank Adaptation of Large Language Models: arXiv preprint arXiv:2106.09685: https://arxiv.org/abs/2106.09685 by Hu et al. (2021).
Please note that the entirity of the Code discussed below is implemented in this Google Colab:
Related Articles
AI Singing Voice Cloning With AI In Python
Finetuning Your Own Custom Stable Diffusion Model With Just 4 Images
Finetuning LayoutLMv2 For Document Question Answering

Newsletter