Buying Losers and Selling Winners In Python in the Modern Digital Era
Have you ever overreacted to something, later reflecting and thinking, ‘Maybe I went a bit overboard’? Now, imagine the stock market — a vast, complex entity influenced by countless decisions made every second — doing the same thing. Getting caught up in the frenzy of news, events, and sentiments, and perhaps swinging more dramatically than the situation warrants.
Back in 1985, De Bondt and Thaler asked a similar question with their paper, “Does the Stock Market Overreact?” that challenged the longstanding efficient market hypothesis (EMH). The EMH, in its essence, postulates that stock prices reflect all available information, implying a nearly impossible task of consistently outperforming the market through either expert analysis or sheer luck.
Revisiting Market Overreactions
De Bondt and Thaler, through their research, suggested otherwise. They argued that the market, driven by human investors, might sometimes swing to extremes — overreacting to both good and bad news. Their seminal work laid the foundation for what we now know as behavioral finance, a field that delves deep into the psychological intricacies of investor decisions.

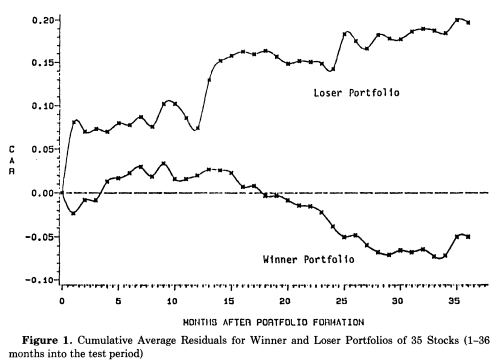
Figure 1. Abstract of the seminal 1985 paper ‘Does the Stock Market Overreact?’ by De Bondt and Thaler, alongside their iconic graph illustrating the performance divergence between ‘winners’ and ‘losers’ portfolios. (Source: https://www.jstor.org/stable/2327804)
Decades have passed since this influential paper was published, and the financial landscape has dramatically evolved. We’ve witnessed the rise of algorithmic trading, the dot-com bubble, the 2008 financial crisis, and the unprecedented market behaviors of the 2020s. With all these changes and the tools of the digital age at our disposal, one can’t help but wonder:
Does the stock market overreact in this era?
In this article, we attempt to revisit this classic financial conundrum using modern data and tools. While we make no claims of academic rigor or statistical significance, the results are, to say the least, intriguing. Python code is also provided for you to test it yourself.
2. Market Efficiency and Human Psychology
It’s imperative to first understand the backdrop against which De Bondt and Thaler presented their findings. This background sets the stage for our exploration and underscores the significance of the original paper’s findings in relation to “Does Stock Market Overreact?”.
The Efficient Market Hypothesis (EMH):
At the heart of modern financial theory lies the Efficient Market Hypothesis (EMH). In its most basic form, the EMH posits that stock prices instantly and fully reflect all available information. This implies that, at any given time, asset prices are at their “fair value,” making it impossible to consistently outperform the market, whether through expert stock selection or timing.
The EMH assumes that numerous rational profit-seekers in the market actively correct any minor mispricings. Essentially, any new information relevant to an asset’s value would be immediately incorporated into its price.
This hypothesis has three main forms:
- Weak Form: Stock prices reflect all past publicly available information, including past price and volume information. Thus, techniques like technical analysis cannot yield consistent profits.
- Semi-Strong Form: Stock prices adjust rapidly to new public information. Neither technical nor fundamental analysis can ensure above-average returns.
- Strong Form: Stock prices reflect all public and private information, making it impossible for even insiders to gain an edge.
Challenging the EMH: Overreaction and Price Reversals
De Bondt and Thaler’s paper threw a wrench in the traditional understanding of the EMH. They argued that stock prices do not always rationally reflect all available information. Instead, they posited that investor psychology could cause prices to swing excessively in reaction to news or events — in other words, the market tends to overreact.
Their research found patterns suggesting that stocks that had performed exceptionally well or poorly over a given time frame experienced price reversals in subsequent periods. Essentially, “winners” would eventually underperform the market, while “losers” would outperform. This was a direct challenge to the EMH, which would argue against such predictable patterns.
This discovery was monumental. It bridged the gap between psychology and finance, giving birth to the burgeoning field of behavioral finance. This domain seeks to understand how cognitive biases can drive investor decisions and influence market dynamics.
3. Python Implementation Methodology
To properly assess the hypothesis presented by De Bondt and Thaler in the modern age, we employ a mix of financial data analysis, statistical methods, and contemporary trading logic. Let’s discuss the specifics before we present the results
Data Source:
- Fetching with yfinance: We used
yfinance, a Python library that sources historical stock data directly from Yahoo Finance.
import yfinance as yf
- Time Frame: The focus lies between 2010 and 2023, ensuring we capture the latest market behaviors while maintaining a broad enough window for meaningful insights.
data = yf.download(tickers, start="2010-01-01", end="2023-21-09")['Adj Close']
- Tickers: Our analysis revolves around some of the most prominent names in the corporate world. From tech giants like Apple (
AAPL), Microsoft (MSFT), and Alphabet (GOOGL), to stalwarts in various sectors such as Pfizer (PFE), Coca-Cola (KO), and Boeing (BA), our selection includes a diverse mix of 40 corporations. These companies, in many ways, can be seen as a microcosm of the larger market, making them excellent candidates for this study. They are all part of the SP&500.
tickers = [
'AAPL', # Apple Inc.
'MSFT', # Microsoft Corp.
'GOOGL', # Alphabet Inc. (Google)
'AMZN', # Amazon.com Inc.
'META', # META Inc.
'TSLA', # Tesla Inc.
'BRK-B', # Berkshire Hathaway Inc.
'NVDA', # NVIDIA Corp.
'JPM', # JPMorgan Chase & Co.
'JNJ', # Johnson & Johnson
'V', # Visa Inc.
'PG', # Procter & Gamble Co.
'UNH', # UnitedHealth Group Inc.
'MA', # Mastercard Inc.
'DIS', # Walt Disney Co.
'HD', # Home Depot Inc.
'BAC', # Bank of America Corp.
'VZ', # Verizon Communications Inc.
'PYPL', # PayPal Holdings Inc.
'ADBE', # Adobe Inc.
'CMCSA', # Comcast Corp.
'NFLX', # Netflix Inc.
'KO', # Coca-Cola Co.
'NKE', # Nike Inc.
'MRK', # Merck & Co Inc.
'PFE', # Pfizer Inc.
'WMT', # Walmart Inc.
'T', # AT&T Inc.
'PEP', # PepsiCo Inc.
'INTC', # Intel Corp.
'CSCO', # Cisco Systems Inc.
'COST', # Costco Wholesale Corp.
'ABBV', # AbbVie Inc.
'NEE', # NextEra Energy Inc.
'MDT', # Medtronic Plc.
'TXN', # Texas Instruments Inc.
'GE', # General Electric Co.
'ACN', # Accenture Plc.
'QCOM', # Qualcomm Inc.
'LLY', # Eli Lilly and Co.
'MCD', # McDonald's Corp.
'DHR', # Danaher Corp.
'AVGO', # Broadcom Inc.
'LIN', # Linde Plc.
'CRM', # Salesforce.com Inc.
'BA' # Boeing Co.
]
Z-scores & Significance:
- The Role of Z-scores: In statistics, a Z-score indicates how many standard deviations an element is from the mean. In our analysis, this helps identify extreme stock returns, be they positive or negative.
mean = returns.rolling(window=252).mean()
std = returns.rolling(window=252).std()
z_scores = (returns - mean) / std
- Thresholds Explained: The thresholds of -1.5 and 1.5 were chosen to capture the most extreme daily price movements, representing the top 6.68% of unusual price swings. In this context, stocks with Z-scores below -1.5 are identified as potential “losers,” indicating they’ve underperformed significantly. Conversely, those with Z-scores above 1.5 are seen as potential “winners,” having demonstrated notable outperformance.
buy_signals = z_scores < -1.5
sell_signals = z_scores > 1.5
If you want to know more about how to use Z-Scores for identifying potential buy and sell signals, consider implementing the techniques discussed in the following article:
Analyzing Rolling Z-Scores In Stock Trading With Python
Building Portfolios:
- Capturing Extremes: We construct two portfolios using the Z-score thresholds. One that “buys” the losers (those the market might have overly punished) and another that “sells” the winners (those possibly riding a wave of excessive optimism).
winners_portfolio = pd.DataFrame(...)
losers_portfolio = pd.DataFrame(...)
- Holding Period: After buying a loser or selling a winner, a holding period of 60 days (approximately 3 months) is observed before liquidating the position. This duration allows the market ample time for potential corrections, either from over-pessimism or over-optimism.
holding_period = 60
- Position Logic: For each stock and trading day, positions are entered based on the buy or sell signals. These positions are held for the predefined period, ensuring we capture any potential reversals post overreaction.
for ticker in tickers:
...
Visualization
Finally, we visualize the cumulative returns of both portfolios to grasp the implications of our strategy fully. This graphical representation provides a clear picture of how buying losers and selling winners would have performed over the selected time frame.
Putting it all together we get the following graph:
import yfinance as yf
import pandas as pd
import matplotlib.pyplot as plt
# Fetch data
data = yf.download(tickers, start="2010-01-01", end="2024-01-01")['Adj Close']
returns = data.pct_change().dropna()
# Calculate z-scores with a 252-day rolling window
mean = returns.rolling(window=252).mean()
std = returns.rolling(window=252).std()
z_scores = (returns - mean) / std
buy_signals = z_scores < -1.5
sell_signals = z_scores > 1.5
holding_period = 60
# Portfolios to hold our positions
winners_portfolio = pd.DataFrame(index=returns.index, columns=returns.columns).fillna(0.0)
losers_portfolio = pd.DataFrame(index=returns.index, columns=returns.columns).fillna(0.0)
for ticker in tickers:
position = 0 # -1 for short, 0 for neutral, 1 for long
days_held = 0
for date, value in returns[ticker].iteritems():
if days_held > 0:
days_held -= 1
if days_held == 0:
position = 0
if buy_signals[ticker][date] and position == 0:
losers_portfolio.at[date, ticker] = 1
position = 1
days_held = holding_period
elif sell_signals[ticker][date] and position == 0:
winners_portfolio.at[date, ticker] = -1
position = -1
days_held = holding_period
# Daily Portfolio Returns
winners_returns = winners_portfolio.shift(1) * returns
losers_returns = losers_portfolio.shift(1) * returns
# Cumulative Portfolio Returns
cumulative_winners_returns = (1 + winners_returns).cumprod().mean(axis=1) - 1
cumulative_losers_returns = (1 + losers_returns).cumprod().mean(axis=1) - 1
# Plotting
plt.figure(figsize=(25, 8))
cumulative_winners_returns.plot(label="Winners Portfolio")
cumulative_losers_returns.plot(label="Losers Portfolio")
plt.title("Cumulative Returns of Winners and Losers Portfolio", fontsize = 20)
plt.legend(fontsize = 20)
plt.show()

Newsletter