Volatility Signature Analysis To Separate Noise from Signal
Volatility Signature Analysis for Intraday Noise Decomposition and to Detect Market Microstructure Distortion in Python
Volatility is one of the most important concepts in markets. We use it to manage risk, forecast returns, and price options.
But there’s a problem — most of what we observe in high-frequency data isn’t real volatility.
It’s noise.
Bid-ask spreads, order flow imbalances, and execution latency all inflate short-term return variation.
This distortion makes it easy to misinterpret risk, especially when backtesting intraday strategies or analyzing realized volatility.
In this article, we show how to separate market signal from microstructure noise using real intraday and long-term open-source data. Along the way, we’ll cover:
- How volatility scales with time — and what it tells us about market efficiency
- A model that quantifies the noise in high-frequency price data
- Why implied volatility (VIX) consistently overestimates realized volatility
- How volatility changes by hour of day and day of week
2. Volatility Signature Across Time Scales
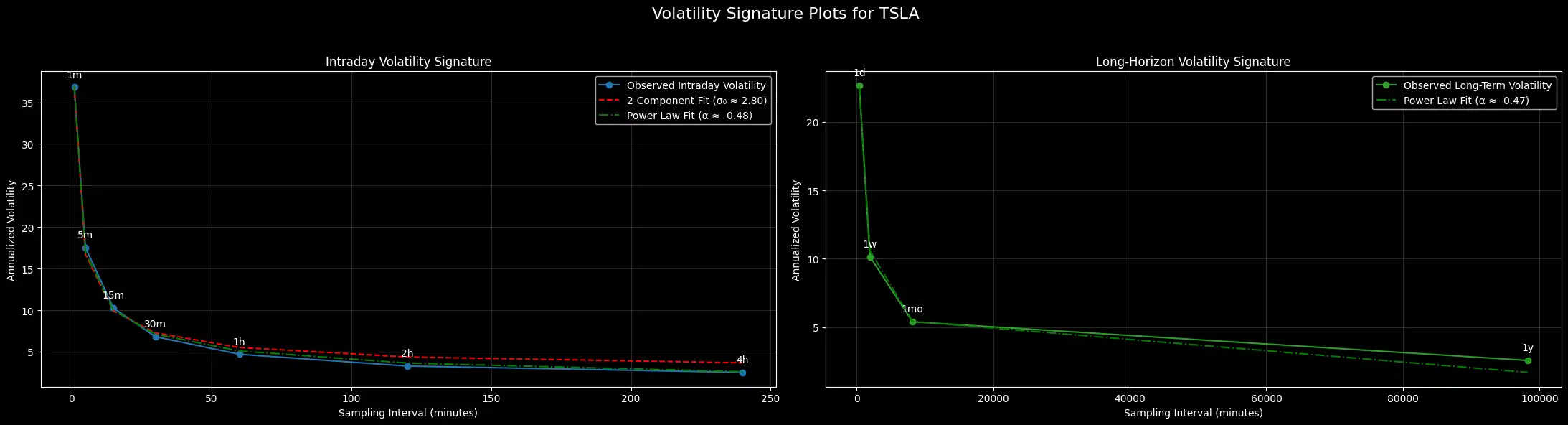
How does volatility behave when we change the lens through which we observe the market?
If you measure Tesla’s volatility every minute, you’ll find it erratic and jumpy.
But zoom out to weekly or monthly intervals, and things begin to smooth out. What’s happening here is structure. And that structure can be modeled.
Let’s build volatility signature plots using both intraday and long-horizon data.
These plots reveal how volatility decays with time, and more importantly, whether that decay is driven by meaningful market dynamics or distorted by noise.
2.1 Power-law model
Volatility is not scale-invariant — it compresses as you aggregate returns over time. This decay often follows a power-law form:
- T is the sampling interval (e.g. 1 minute, 1 day),
- c is the scale factor (volatility at unit time),
- α is the scaling exponent that governs how volatility decays.
What does α tell us?
- α = 0.5: Classic Brownian motion (efficient markets).
- α < 0.5: Fast decay, often due to microstructure noise at high frequencies.
- α > 0.5: Slow decay, potentially reflecting volatility persistence or memory.
Fitting this model across both intraday and long-horizon data quantifies the rate at which markets “smooth out” over time.
2.2 Two-component model
Short-term volatility is often inflated by noise — order book imbalances, bid-ask spreads, execution slippage.
To separate signal from noise, we use a two-component model:
- 0² is the true underlying variance (signal),
- η² is the microstructure noise component,
- T is the sampling interval in minutes.
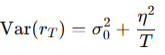
This model helps us identify the minimum volatility floor 0² and quantify how much observed variation is due to meaningless noise.
As T increases, the noise term decays and we converge toward the latent signal.
2.3 Python Implementation
Below is the implementation for both models using 1-minute intraday data and daily OHLC data for TSLA.
We fit both models to the intraday signature, and only the power-law model to long-horizon data.
import yfinance as yf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
from scipy.optimize import curve_fit
plt.style.use('dark_background')
Newsletter